11 Proof Techniques
Throughout our educational experiences we have been asked to show our work. In arithmetic we showed how ![]() , in geometry we found the length of the hypotenuse of a triangle, and in calculus we showed our steps to evaluate an integral or take a derivative. In analysis we are asked to show our work for how we came to a conclusion, using proofs. We begin by being given a statement or claim that we are asked to prove using our statements take on the form
, in geometry we found the length of the hypotenuse of a triangle, and in calculus we showed our steps to evaluate an integral or take a derivative. In analysis we are asked to show our work for how we came to a conclusion, using proofs. We begin by being given a statement or claim that we are asked to prove using our statements take on the form ![]() . We have seen this notation before, in logic we learned that this denotes an “if, then” statement. In order to prove a statement like this, we are required to provide a proof. As mentioned above, a proof is a structured walk through the steps taken and theorems applied to come to the suggested conclusion or or to disprove the claim entirely. Much like a debate there are several different structure we can apply to create our proof.
. We have seen this notation before, in logic we learned that this denotes an “if, then” statement. In order to prove a statement like this, we are required to provide a proof. As mentioned above, a proof is a structured walk through the steps taken and theorems applied to come to the suggested conclusion or or to disprove the claim entirely. Much like a debate there are several different structure we can apply to create our proof.
There are five proof techniques we will cover: direct proofs, proof by contraposition, indirect proofs, mathematical induction, and proof by cases. We will introduce each technique in detail below.
10.1 Direct Proofs
Direct proofs are just that, direct. Given the claim ![]() , we begin with allowing
, we begin with allowing ![]() to be true, then by utilizing known theorems and logic we work to a conclusion that either concludes
to be true, then by utilizing known theorems and logic we work to a conclusion that either concludes ![]() to be true or disproves
to be true or disproves ![]() . The formal steps for direct proof are as follows.
. The formal steps for direct proof are as follows.
- Assume that
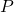 is true
is true - Use
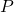 to show that
to show that 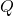 must be true
must be true
From these steps we know that in order to prove a claim directly we must utilize what information we are given from our statement ![]() , knowing that the claim
, knowing that the claim ![]() is structured as “if
is structured as “if ![]() , then
, then ![]() “. From this step we move to prove that
“. From this step we move to prove that ![]() is true by utilizing theorems and definitions that lead us to the conclusion that
is true by utilizing theorems and definitions that lead us to the conclusion that ![]() is true, and thus
is true, and thus ![]() . We can see an example of this proof technique in use, below.
. We can see an example of this proof technique in use, below.
Example:
The sum of two odd numbers is even.
Proof: Let ![]() ,
, ![]() be odd, by the definition of odd numbers there exists
be odd, by the definition of odd numbers there exists ![]() such that
such that ![]() and
and ![]() . Then,
. Then,
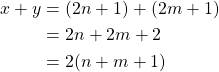
Now let ![]() where
where ![]() , since
, since ![]() which is closed under addition. Thus,
which is closed under addition. Thus,
![]()
for ![]() . Therefor, by the definition of even numbers
. Therefor, by the definition of even numbers ![]() is even
is even
Let’s now move to the next proof technique which takes the counter approach to a direct proof.
10.2 Contraposition
Previously in the section on direct proofs, we discussed the “if, then” statement. With direct proofs we approach this by claiming ![]() to be true and thus prove
to be true and thus prove ![]() to be true. We denoted this form of proof by
to be true. We denoted this form of proof by ![]() , with contraposition we denote the proof as
, with contraposition we denote the proof as ![]() . We prove a claim using the contrapositive proof method by claiming
. We prove a claim using the contrapositive proof method by claiming ![]() to be false firstly and then prove
to be false firstly and then prove ![]() to be false. In some ways this is the reverse approach to direct proofing. We provide the steps for contraposition below.
to be false. In some ways this is the reverse approach to direct proofing. We provide the steps for contraposition below.
- Beginning with the implication
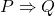 , we first deny
, we first deny 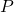 and
and 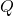 are true, denoted by
are true, denoted by 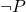 and
and 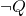 . We are thus, assuming that
. We are thus, assuming that 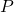 and
and 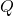 are false.
are false. - Next, directly prove that
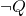 implies
implies 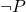 .
.
We are proving a claim, essentially, by proving an alternate position. Consider an example of contrapositive application.
Example:
If ![]() is even, then
is even, then ![]() is odd.
is odd.
Proof: Consider that ![]() is even, by the definition of even numbers there is
is even, by the definition of even numbers there is ![]() such that
such that ![]() . Thus we can rewrite
. Thus we can rewrite ![]() as follows:
as follows:
![]()
If we consider that
![]()
then we can factor out ![]() from
from ![]() which gives us the following result
which gives us the following result
![]()
Since ![]() which is closed under addition, let
which is closed under addition, let ![]() where
where ![]() such that
such that
![]()
for ![]() . Therefore by the definition of odd numbers
. Therefore by the definition of odd numbers ![]() is odd.
is odd.
We can see here in this example that we began the proof with the claim that “![]() is odd” is false and from there we structured a proof that proved the negative of the statement “
is odd” is false and from there we structured a proof that proved the negative of the statement “![]() is even” as proposed by proof by contraposition. Now in some courses contraposition proofs fall under the category Indirect proofs because the proof does not follow a direct path from assumption to conclusion. Here we only categorize contrapositive proofs as indirect proofs but it should be noted that both contrapositive and contraposition in most cases are both considered indirect proofs.
is even” as proposed by proof by contraposition. Now in some courses contraposition proofs fall under the category Indirect proofs because the proof does not follow a direct path from assumption to conclusion. Here we only categorize contrapositive proofs as indirect proofs but it should be noted that both contrapositive and contraposition in most cases are both considered indirect proofs.
10.3 Indirect Proofs
Indirect proofs, like we have seen in contrapositive proofs, find alternative ways to prove a claim. We utilize indirect proofs when proving a claim directly is too challenging. The idea behind indirect proofs is that we want to prove all other possibilities are impossible and thus our claim must be true. Under indirect proofs we will discuss the proof by contradiction. When we start a proof by contradiction we begin by assuming our statement ![]() is not true. We then work through our proof using definitions and theorems to conclude
is not true. We then work through our proof using definitions and theorems to conclude ![]() which is a contradiction. Consider the below example.
which is a contradiction. Consider the below example.
Example:
Prove that ![]() is irrational [20].
is irrational [20].
Proof: Assume ![]() is a rational number, let
is a rational number, let ![]() where
where ![]() and
and ![]() share no common factors. If
share no common factors. If ![]() then
then ![]() which suggests that
which suggests that ![]() is a multiple of
is a multiple of ![]() , a prime number, therefore
, a prime number, therefore ![]() is divisible by the prime number
is divisible by the prime number ![]() . Next, we can say that
. Next, we can say that ![]() contains an even number of prime factors given that
contains an even number of prime factors given that ![]() will contain an even number of prime factors. We can rewrite
will contain an even number of prime factors. We can rewrite ![]() then to be
then to be ![]() for
for ![]() such that
such that
![]()
Since ![]() then we have the equality
then we have the equality
![]()
We can then divide both sides by 5 to get
![]()
We can see here that ![]() is a multiple of prime
is a multiple of prime ![]() . Since
. Since ![]() and
and ![]() contains an even number of prime factors there is
contains an even number of prime factors there is ![]() such that
such that ![]() . Thus
. Thus ![]() and
and ![]() share the common factor
share the common factor ![]() . But
. But ![]() and
and ![]() contain no common factors, this is a contradiction. Thus we conclude that
contain no common factors, this is a contradiction. Thus we conclude that ![]() is an irrational number.
is an irrational number.
We can see in this example that we solved by first assuming ![]() was rational and then proving to a conclusion that contradicted a previously stated claim, thus disproving the argument and allowing us to conclude that
was rational and then proving to a conclusion that contradicted a previously stated claim, thus disproving the argument and allowing us to conclude that ![]() must be irrational.
must be irrational.
Concluding this section we can derive the following steps for a proof by contradiction, as seen in the above examples.
- We are asked to prove
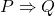
- Assume
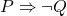 , this implication means if
, this implication means if 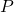 is true then not
is true then not 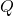 .
. - we then work through a proof to conclude
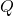 , this is a contradiction.
, this is a contradiction. - Finally, conclude that
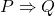 must be true.
must be true.
Let us now move on to another method of proofing that does not prove a statement directly but does not qualify as an indirect proof either. As we will see below there is yet another direction for constructing a proof, from the inside out.
10.4 Mathematical Induction
Some proofs can be structured by proving two cases. This means that we can start with one case, called the base case, which we attempt to prove. If we can prove the base case then, through repeated inductive steps, we can prove that the related cases are true. This leads us to finally conclude that the claim we wanted to prove is true. This method is only effective when the statement, or claim, is true for base case ![]() and when the claim is true for some natural number
and when the claim is true for some natural number ![]() which leads to
which leads to ![]() cases to be true. We call mathematical induction and can be seen in the formal steps to solve prove our below [36].
cases to be true. We call mathematical induction and can be seen in the formal steps to solve prove our below [36].
- The Base Case: The statement is true for case
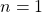 .
. - Inductive Step: If the statement is true for case
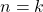 , then the statement is also true for case
, then the statement is also true for case 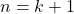 .
.
First consider an example of a direct proof solved by mathematical induction.
Example:
![]() is divisible by 3 [20].
is divisible by 3 [20].
- Base case: Let
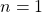 ,
, 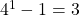 which is divisible by 3 as our claim suggests.
which is divisible by 3 as our claim suggests. - Inductive step: Let
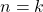 for some
for some 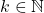 such that
such that 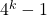 is divisible by
is divisible by 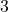 . Then
. Then 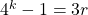 for some
for some 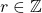 .Consider there is
.Consider there is 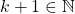 where
where
![]()
Since ![]() then substitute
then substitute ![]() for
for ![]() in our function
in our function
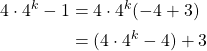
We can factor out 4 from ![]() to get the following
to get the following
![]()
Since ![]() then we can substitute
then we can substitute ![]() with
with ![]() and then simplify by factoring out the common factor.
and then simplify by factoring out the common factor.
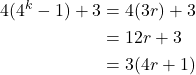
Since we have found ![]() and
and ![]() is divisible by
is divisible by ![]() then we conclude that the product of
then we conclude that the product of ![]() is divisible by 3 as well. Thus since our claim is true whenever
is divisible by 3 as well. Thus since our claim is true whenever ![]() for some
for some ![]() and if the claim is true for
and if the claim is true for ![]() then it is also true for
then it is also true for ![]() , we can conclude that
, we can conclude that ![]() is divisible by 3 for all
is divisible by 3 for all ![]() .
.
By starting small and proving a base case we can use that base case to build on our proof until we can come to a sound conclusion. Induction is a key part of mathematics, we are asked to look at numbers, to find patterns or trends. By locating a pattern or trend between a few examples we can develop a method or law that includes every possible case. We can also develop methods for finding the minimum or maximum steps required to obtain a certain result. An incredible example of this is the Tower of Hanoi problem.
Example: The Tower of Hanoi
There are seven disks, of varying sizes, with holes in the center large enough to fit on each of three posts. We start with all seven disks on one post, all seven disks are stacked in order of largest at the bottom to smallest at the top. The objective is to find the least amount of steps required to move all seven disks onto another peg in the same order. There are two rules that must be followed [25]:
- The only action that can be taken is to move the top disk from one post to another.
- A larger sized disk cannot stack on top of a smaller disk, ever.
In order to solve this problem we need to use induction. We begin with the base step.
Base step: Consider we have one disk, ![]() , and let
, and let ![]() be defined as the minimal number of steps required to move all disks to another peg. The number of steps required to move the disks from one post to another is then
be defined as the minimal number of steps required to move all disks to another peg. The number of steps required to move the disks from one post to another is then
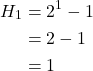
Inductive Step: Now consider ![]() disks, we start by breaking down the steps. The first step would be to move
disks, we start by breaking down the steps. The first step would be to move ![]() disks to another post which requires
disks to another post which requires ![]() moves. Next we consider moving the last disk from the original post to the only other available post without the other disks on it, this requires
moves. Next we consider moving the last disk from the original post to the only other available post without the other disks on it, this requires ![]() moves. Finally we need to move that original stack of
moves. Finally we need to move that original stack of ![]() disks from their second post and onto the post with the largest disk just dropped on it, this will require
disks from their second post and onto the post with the largest disk just dropped on it, this will require ![]() moves. Now lets add these steps to to find the total amount of moves required.
moves. Now lets add these steps to to find the total amount of moves required.
![]()
The last step is to show that ![]() for any
for any ![]() . We already know that
. We already know that ![]() applies to
applies to ![]() , now let
, now let ![]() such that
such that ![]() , using the equation we found above for
, using the equation we found above for ![]() disks substitute
disks substitute ![]() for
for ![]() giving us
giving us ![]() , we solve for
, we solve for ![]() .
.
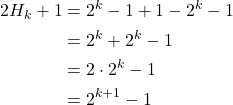
Thus we can conclude that the minimum number of moves required to satisfy the problem given ![]() discs is
discs is ![]() .
.
We have seen from this example that by starting with the most basic case we know to be true we are able to derive a conclusion for all cases by using mathematical induction. And as such we can construct a proof that can prove all cases for a claim.
There is another way to prove a claim through cases when there are only a few cases and each can be solved directly. We see this type of proof introduced below.
10.5 Proof by Cases
As noted in the previous section there are some claims that require a proof for each individual case for the claim. We call this technique proof by cases or in some classes it will be described as proof by exhaustion. The second description sums up the fundamental idea behind a proof by cases. We are given a claim with which we must either prove all possible cases in order to draw a conclusion for the claim entirely. By doing this we leave no room for error in our conclusion because we have considered every possibility and proven its truth value.
Unlike the proof by induction technique, proof by cases does not make any assumptions unless a rational connection can be proven for connecting the truth value of one case to another. There may be proof by induction used per claim but unless a connection can be drawn between claims each claim as proven independently.
Consider an example of this type of proof in use.
Example:
![]() , for
, for ![]() .
.
We will construct our proof using cases.
Case 1) Suppose ![]() if
if ![]() , then
, then ![]() and
and ![]() such that
such that
![]()
This is because the absolute value of positive values in a fraction taken independently, still results in a positive value for the fraction. This is equal to if we were to take the absolute value of the fraction in it’s entirety. As well, if ![]() then
then ![]() such that
such that
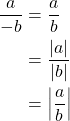
We see here that the absolute value of a negative variable is equal to the variable if it were simply positive. Thus, we find that the absolute value of the denominator and numerator, found separately, is equal to the absolute value of the fraction if we took the absolute value of the fraction as a whole. Therefore we can conclude that ![]() for
for ![]() and
and ![]() or
or ![]() .
.
Case 2) Suppose ![]() and
and ![]() , then
, then ![]() and
and ![]() , thus
, thus
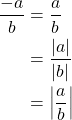
If ![]() , then
, then ![]() and
and ![]() , thus
, thus
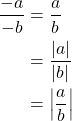
Here we see that the absolute value of a negative variable is equal to the variable if it were simply positive. Thus the absolute value of the numerator and denominator, found separately, is equal to the absolute value of the fraction. Therefore we can conclude that ![]() for
for ![]() and
and ![]() or
or ![]() .
.
Case 3) Suppose ![]() and
and ![]() , then
, then ![]() and
and ![]() , thus
, thus
![]()
If ![]() , then
, then ![]() , thus
, thus
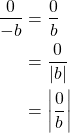
Since 0 is never negative and the absolute value of a variable, negative or positive, results in a positive, then we can conclude that absolute value of the denominator and numerator, found individually, is the same as if we were to take the absolute value of the fraction as a whole. Thus we can make the final conclusion that the initial claim is true since every case has been proven to be true.
Proofs by cases are a great way to prove a claim when applicable. Without being able to address each case individually we would not be able to prove without a doubt that our claim was true.
