26 Rings
In the previous sections we looked at sets with one binary operation, in this section we will be looking at sets with two binary operations.
Definition.
A ring ![]() is a set
is a set ![]() together with two binary operations + and
together with two binary operations + and ![]() , defined on
, defined on ![]() such that the following axioms are satisfied:
such that the following axioms are satisfied:
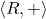 is an abelian group.
is an abelian group.- Multiplication is associative
- For all
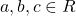 , the left distributive law,
, the left distributive law, 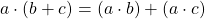 and the right distributive law
and the right distributive law 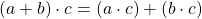 hold.
hold.
Here we are introduced to two new terms, the left and right distributive laws. These laws are the structural requirements for how two binary operations, addition and multiplication, are applied to the set ![]() .
.
Being Abstract Algebra there is always additional properties to categorize a structure further. We can categorize rings in the following ways:
The Commutative Ring: A ring in which the multiplication is commutative is known as a commutative ring.
Ring with Unity: A ring with the multiplicative identity element 1, which we call “unity” in abstract algebra, is known as a ring with unity [12].
Division Ring: Let element ![]() in ring
in ring ![]() , with unity, be a unit of
, with unity, be a unit of ![]() if
if ![]() has a multiplicative inverse in
has a multiplicative inverse in ![]() . If every nonzero element of
. If every nonzero element of ![]() is a unit, then
is a unit, then ![]() is a division ring.
is a division ring.
Field: A field is a commutative division ring.
There is little further explanation needed for these different categorizations of rings since we are already familiar with the terms and the algebraic operations that define each. Now we can observe how we might go about finding a ring as well as categorizing it using the above terms.
Example:
Decide whether ![]() with the usual addition and multiplication are closed on the set, give a ring structure. If a ring is formed, state whether the ring is commutative, has unity, and is a field [12].
with the usual addition and multiplication are closed on the set, give a ring structure. If a ring is formed, state whether the ring is commutative, has unity, and is a field [12].
- Let
 then we have
then we have 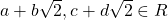 such that
such that
![]()
and thus we can conclude that ![]() is closed under addition.
is closed under addition.
- Let
 then we have
then we have 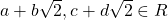 such that
such that
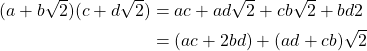
Where ![]() , thus we can conclude that
, thus we can conclude that ![]() is closed under multiplication. Thus we have proven
is closed under multiplication. Thus we have proven ![]() is closed for addition and multiplication.
is closed for addition and multiplication.
Thus we have proven ![]() is closed for addition and multiplication. Now consider that
is closed for addition and multiplication. Now consider that ![]() is a ring, we need to satisfy all three axioms for a ring.
is a ring, we need to satisfy all three axioms for a ring.
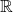 is an abelian group under addition and it has been proven that
is an abelian group under addition and it has been proven that 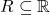 such that for all
such that for all 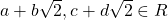 it follows that
it follows that
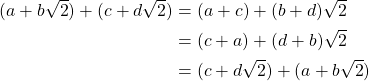
thus we conclude that ![]() is an abelian group.
is an abelian group.
- Given
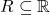 then elements of
then elements of 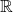 are also elements of
are also elements of 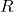 and since
and since 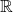 is associative then we can conclude that multiplication on ring
is associative then we can conclude that multiplication on ring 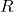 is associative.
is associative. - Given
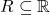 then since the right and left distribution laws hold for
then since the right and left distribution laws hold for 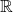 then they hold for
then they hold for 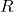 .
.
Thus we can conclude that ![]() is a ring.
is a ring.
Now since ![]() is commutative then the multiplication on
is commutative then the multiplication on ![]() is commutative, thus
is commutative, thus ![]() is a commutative ring.
is a commutative ring.
Let 1 be the identity element in ![]() under multiplication such that
under multiplication such that ![]() and thus
and thus ![]() for all
for all ![]() . We can thus conclude that
. We can thus conclude that ![]() is a ring with unity 1.
is a ring with unity 1.
Let ![]() then
then ![]() is a non-zero element of the field
is a non-zero element of the field ![]() so the inverse
so the inverse ![]() . We can rationalize this as
. We can rationalize this as
![]()
Since ![]() then
then ![]() and so we can write
and so we can write ![]() for which
for which
![]()
Thus ![]() is a field.
is a field.
We should now have a good understanding from the above example, about how to find rings as well as how to prove their commutative, unity, division, and field property. There is so much more to discover about rings in Abstract Algebra, how they apply to polynomials, the concept of sub-rings and how they apply to our next topic, fields. In the next section we will look at fields a bit more and look at some more examples with a stronger focus on fields.
22.1 Fields
We have already given the brief description that a field is a ring which satisfies both the commutative property and the property for division ring. But fields deserve their own formal definition and axioms [12].
Definition.
Let ![]() be a group with two binary operations, + and
be a group with two binary operations, + and ![]() , with respect to the following axioms:
, with respect to the following axioms:
- For all k
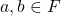 it follows that
it follows that 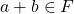 and
and 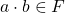 such that
such that 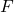 is closed under addition and multiplication.
is closed under addition and multiplication. - For all
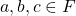 it follows that
it follows that 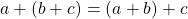 and
and 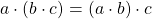 such that
such that 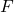 is associative.
is associative. - For all
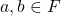 it follows that
it follows that 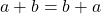 and
and 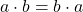 such that both addition and multiplication under
such that both addition and multiplication under 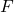 is commutative.
is commutative.
We can see from this definition that a field is a set that satisfies the axioms for a group, as well as satisfying every commutative property so that a field ![]() is a commutative ring. Let us now introduce a few structural classifications for fields [12].
is a commutative ring. Let us now introduce a few structural classifications for fields [12].
Theorem: Field of Quotients of ![]()
Any integral domain ![]() can be enlarged to a field
can be enlarged to a field ![]() such that every element of
such that every element of ![]() can be expressed as a quotient of two elements of
can be expressed as a quotient of two elements of ![]() .
.
It should be noted from this theorem that every field ![]() containing an integral domain
containing an integral domain ![]() contains a field of quotients of
contains a field of quotients of ![]() . This is a similar rule to cyclic subgroups where every group has within it a cyclic subgroup. This comparison tells us there are so many structural similarities and axioms that carry over to different categories that a set may qualify under. We truly can see that Abstract Algebra is all about the study of set structure and the properties that help to classify them. Being able to classify sets helps mathematicians be able to instantly understand the properties of a set depending on whether they are a ring, group, field, subgroup, etc. Just as in rings and groups, fields have underlying structures [12].
. This is a similar rule to cyclic subgroups where every group has within it a cyclic subgroup. This comparison tells us there are so many structural similarities and axioms that carry over to different categories that a set may qualify under. We truly can see that Abstract Algebra is all about the study of set structure and the properties that help to classify them. Being able to classify sets helps mathematicians be able to instantly understand the properties of a set depending on whether they are a ring, group, field, subgroup, etc. Just as in rings and groups, fields have underlying structures [12].
Theorem:
For ![]() and
and ![]() in
in ![]() , the equations
, the equations ![]() and
and ![]() give well-defined operations of addition and multiplication on
give well-defined operations of addition and multiplication on ![]() .
.
Here, we can see the structure for elements of a set under field multiplication and addition. If we observe the above theorem we see that when we sum equivalence classes ![]() and
and ![]() , which are arbitrary classes in
, which are arbitrary classes in ![]() the axiom states that the sum is equivalent to
the axiom states that the sum is equivalent to ![]() . Under each operation never can
. Under each operation never can ![]() or for that matter
or for that matter ![]() or
or ![]() . Just as we have seen before throughout our study of mathematics, there are always axioms for binary operations. Fields, as we can see are no different. We can see an example of how we might apply these axioms to a problem, below, to prove that a field
. Just as we have seen before throughout our study of mathematics, there are always axioms for binary operations. Fields, as we can see are no different. We can see an example of how we might apply these axioms to a problem, below, to prove that a field ![]() also contains identity elements and inverse elements under addition and multiplication.
also contains identity elements and inverse elements under addition and multiplication.
Example:
Now ![]() is by definition
is by definition ![]() . Also
. Also ![]() is by definition
is by definition ![]() . Prove that
. Prove that ![]() is an identity element for addition in
is an identity element for addition in ![]() . Prove
. Prove ![]() is an additive inverse for
is an additive inverse for ![]() in
in ![]() .
.
Consider ![]() such that
such that
![]()
thus we can conclude that ![]() is an identity element for addition in
is an identity element for addition in ![]() . Now consider
. Now consider ![]() such that
such that
![]()
and since ![]() then
then ![]() and if
and if
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} [(a,b)]+[(-a,b)]&=[(ab+b(-a), b^{2})]\\ &=[(ab-ba, b^{2})]\\ &=[(0,b^{2})]=[(0,1)] \end{split} \end{equation*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c1163a42f26b70340fd7d97ec53ea120_l3.png)
thus we can conclude that ![]() is an additive inverse for
is an additive inverse for ![]() .
.
Here we can make out similarities between groups, rings, and fields. Although the structure for addition and multiplication, as it pertains to each category, is formatted specifically for a group, a ring, or a field we have some commonalities. Each group, ring, and field must contain an inverse element and an identity element under the one or two binary operations applied to it. From this last example we saw that elements of fields can be expressed as ![]() . These are called equivalence classes and
. These are called equivalence classes and ![]() is considered the set of all equivalence classes for two elements
is considered the set of all equivalence classes for two elements ![]() where
where ![]() is a set. We can further explain that an equivalence class
is a set. We can further explain that an equivalence class ![]() is for
is for ![]() in
in ![]() under the relation
under the relation ![]() . There are three properties for an equivalence relation [12]:
. There are three properties for an equivalence relation [12]:
- Reflexive Let
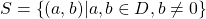 then
then 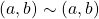 since
since 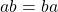 for multiplication in
for multiplication in 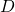 , where
, where 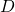 is the integral domain.
is the integral domain. - Symmetric If
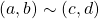 , then
, then 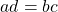 . Since multiplication in
. Since multiplication in 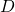 is commutative then
is commutative then 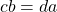 thus resulting in
thus resulting in 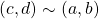 .
. - Transitive If
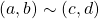 , and
, and 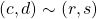 , then
, then 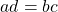 and
and 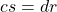 . Since
. Since 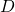 is commutative, we have
is commutative, we have 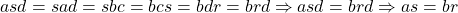 and thus
and thus 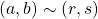
We should already be familiar with the concepts of reflexive, symmetric, and transitive from our discussion of set theory so the notion that these same properties can apply for an equivalence class of a set should seem straight forward.
Before we move on to the next topic, observe the following example that helps to relate sub-domains to domains using the properties for a field of quotients [12].
Example:
Show by an example that a field ![]() of quotients of a proper sub-domain
of quotients of a proper sub-domain ![]() of an integral domain
of an integral domain ![]() may also be a field of quotients for
may also be a field of quotients for ![]() .
.
Let ![]() be an integral domain, then
be an integral domain, then ![]() such that
such that ![]() since a rational number formed by two integers is a quotient. Since
since a rational number formed by two integers is a quotient. Since ![]() is a field then
is a field then ![]() . If
. If ![]() is the field of quotients for
is the field of quotients for ![]() then we also say
then we also say ![]() and since
and since ![]() is the field of quotients for
is the field of quotients for ![]() then we can also say that
then we can also say that ![]() thus we can conclude that
thus we can conclude that ![]() . Thus a field of quotients for the sub-domain
. Thus a field of quotients for the sub-domain ![]() is also the field of quotients for integral domain
is also the field of quotients for integral domain ![]() .
.
With such a focus on integral domains in this example, beyond assisting in the definition of a field of quotients, it makes sense to have a separate section to better explain integral domains and their use.
22.2 Integral Domains
We gave a brief introduction to integral domains as the pertain to the definitions for fields but as always there is a formal definition which we will cover here as well as a diagram of how all these terms relate to one another.
Definition. Zero Divisor
If ![]() and
and ![]() are two ring elements with
are two ring elements with ![]() but
but ![]() then
then ![]() and
and ![]() are zero-divisors.
are zero-divisors.
This might not make any sense at first, how could two non zero elements multiplied together, produce the quantity 0? This is easiest to explain by looking at an example.
Example:
Given ![]() in
in ![]() find all the solutions.
find all the solutions.
We address each element in ![]() ;
; ![]() .
.
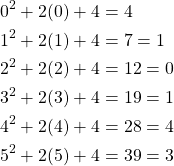
Thus we can conclude that the only solution in ![]() is when
is when ![]() .
.
Here we are given a function in the ring ![]() thus the we can put every result from the function as they relate to 6 since 6 divides 12 evenly we let
thus the we can put every result from the function as they relate to 6 since 6 divides 12 evenly we let ![]() where as since 6 divides 7 with a remainder of 1 we let
where as since 6 divides 7 with a remainder of 1 we let ![]() . With this rough description in mind we introduce a theorem for finding the zero-divisors of a ring.
. With this rough description in mind we introduce a theorem for finding the zero-divisors of a ring.
Theorem:
In the ring ![]() , the divisors of 0 are precisely those nonzero elements that are not relatively prime to
, the divisors of 0 are precisely those nonzero elements that are not relatively prime to ![]() .
.
The counter view to this which supports this theorem is that if ![]() for
for ![]() is prime then
is prime then ![]() has no zero divisor because the only two integers
has no zero divisor because the only two integers ![]() and
and ![]() whose product
whose product ![]() is a prime number is when
is a prime number is when ![]() and
and ![]() where
where ![]() is the prime number such that
is the prime number such that ![]() and since
and since ![]() cannot be an element in
cannot be an element in ![]() then we say
then we say ![]() has no divisor of 0.
has no divisor of 0.
Now that we have introduced the concept of divisors we can introduce integral domains, formally.
Definition.
An integral domain ![]() is a commutative ring with unity
is a commutative ring with unity ![]() and containing no divisors of 0.
and containing no divisors of 0.
This will make more sense when we look at a few examples later on but for now we can see how the definition of an integral domain applies to rings and fields. Now we are familiar with fields by now and we know that fields are commutative rings so it follows that all fields are integral domains and thus every finite integral domain is a field.
Theorem:
If ![]() is a prime, then
is a prime, then ![]() is a field.
is a field.
This theorem holds because ![]() is a finite integral domain since
is a finite integral domain since ![]() is prime and thus
is prime and thus ![]() is also a field. Continuing on our relations between integral domains and other algebraic sets we introduce rings in relation to integral domains [12].
is also a field. Continuing on our relations between integral domains and other algebraic sets we introduce rings in relation to integral domains [12].
Definition. The characteristic of the ring ![]()
If for a ring ![]() a positive integer
a positive integer ![]() exists such that
exists such that ![]() for all
for all ![]() , then the least positive integer is the characteristic of the ring
, then the least positive integer is the characteristic of the ring ![]() . If no such positive integer exists, then
. If no such positive integer exists, then ![]() is of characteristic 0.
is of characteristic 0.
Theorem:
Let ![]() be a ring with unity. If
be a ring with unity. If ![]() for all
for all ![]() , then
, then ![]() has characteristic 0. If
has characteristic 0. If ![]() for some
for some ![]() , then the smallest such integer
, then the smallest such integer ![]() is the characteristic of
is the characteristic of ![]() .
.
Example:
Show that the characteristic of an integral domain ![]() must be either 0 or a prime
must be either 0 or a prime ![]() .
.
Let ![]() be the characteristic of
be the characteristic of ![]() for
for ![]() such that
such that ![]() .
.
Consider the characteristic of ![]() is not prime. Then there exists
is not prime. Then there exists ![]() where
where ![]() and
and ![]() such that the characteristic of
such that the characteristic of ![]() is
is ![]() . If we let
. If we let ![]() be the smallest positive integer such that
be the smallest positive integer such that ![]() for
for ![]() . Then we let
. Then we let
![]()
with ![]() sums of
sums of ![]() with 1 as the unit of ring
with 1 as the unit of ring ![]() . Next
. Next
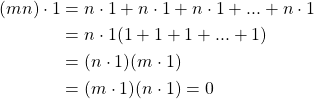
Since ![]() and
and ![]() then by definition for the characteristic of a ring
then by definition for the characteristic of a ring ![]() is not the least positive integer, this is a contradiction to the claim that
is not the least positive integer, this is a contradiction to the claim that ![]() is the characteristic of the integral domain
is the characteristic of the integral domain ![]() . Thus we conclude that the integral domain
. Thus we conclude that the integral domain ![]() has characteristic 0 or prime
has characteristic 0 or prime ![]() .
.
This proof supports the idea that an integral domain, which is itself a ring, has a characteristic of 0 which supports the definition for the characteristic of the ring. As well, this supports the theorem that if a ring or the integral domain has unity then either the characteristic is 0 or it is the smallest positive integer. The characteristic of a ring helps us understand what kind of set we are dealing with if all we are given is the characteristic. The common sets ![]() can all be classified as having a characteristic of 0 because there is no least positive integer in each set because they are infinite.
can all be classified as having a characteristic of 0 because there is no least positive integer in each set because they are infinite.
We will look at one more example, this time with a defined characteristic that is not 0.
Example:
Let ![]() be a commutative ring with unity of characteristic 4. Compute and simplify
be a commutative ring with unity of characteristic 4. Compute and simplify ![]() for
for ![]() [12].
[12].
Let ![]() be a commutative ring with unity of characteristic 4. By the binomial theorem for expansion, for
be a commutative ring with unity of characteristic 4. By the binomial theorem for expansion, for ![]() we have
we have
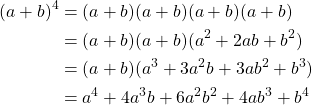
Since we were given that ![]() we can simplify this formula to the following
we can simplify this formula to the following
![]()
Therefore we can conclude that ![]() for all
for all ![]() .
.
In this last example we can see how a characteristic of a ring effects a ring under certain binary operations.
We have now covered groups, various families of rings, integral domains, and fields. In the following diagram we will look at how all these terms relate to one another and how they are all involved with one another.
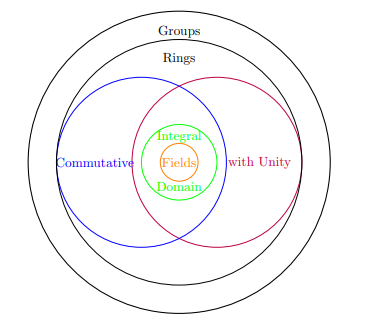
This diagram gives us the best idea for the families under groups and how they all relate to one another. We can also relate the axioms pertaining to each specified ring and how they carry over. This diagram begins with the largest circle which is groups, this means that any inner circle must qualify as a group. If you are asked to prove a set is a field if we can not prove it is first a group then we do not need to go any further. This also means that the axioms that justify a group carry over to every inner family. This diagram shows us that groups are the largest family and with in groups we either have rings or not. With in rings we may have specified commutative rings or rings with unity which sometimes overlap. Within the overlap we have a special family of rings with qualify as integral domains and with in this family some qualify as fields.
Now that we have a strong understanding of how each specified family relates to one another we can look at rings and fields again, this time when determining polynomials.
