Roots

Maggie Schildt

36 Roots

Recall in calculus when you were asked to find the values of $x$ of a function for when $f(x)=0$ . These are what are known as the roots. Most functions we looked at in calculus took on a linear form, but there are nonlinear functions that still require their roots to be calculated. This is where we introduce the Newton-Raphson and the Secant method.

30.1 The Newton-Raphson Method

We will cover the Secant method later on, for now the Newton-Raphson method is given by a formula for which to calculate progressive values that should converge to a root. The formula for calculating the progressive values is given as:

$\begin{equation*} x_{n+1}=x_{n}-\left( \frac{f(x_{n}}{f'(x_{n}} \right) \end{equation*}$

Where $x_{n}$ is the current known value. In the following example we will see how we can analyze the Newton-Raphson method to extrapolate the roots of a nonlinear equation.

Example:

Given the equation $f(x)=\tan(x) - \sin(x) - 2.75=0$ , perform four iterations of the Newton-Raphson method with $x_{0}=1.77$ . [15]

We begin by finding the derivative of $f(x)$ to be $f'(x)=\sec^{2}(x) - \cos(x)$ . Thus we have the following formula for he Newton-Raphson method.

$\begin{equation*} x_{n+1}=x_{n}-\frac{\tan(x) -\sin(x) -2.75}{\sec^{2}(x) -\cos(x)} \end{equation*}$

Now we can calculate the first four iterations starting with $x_{0}=1.77$ .

$\begin{equation*} \begin{split} x_{0+1}=x_{1}&=1.77-\frac{\tan(1.77) -\sin(1.77) -2.75}{\sec^{2}(1.77) -\cos(1.77)}\\ &=2.107436\\ x_{1+1}=x_{2}&=2.107436-\frac{\tan(2.107436) -\sin(2.107436)-2.75}{\sec^{2}(2.107436) -\cos(2.107436)}\\ &=3.327243\\ x_{2+1}=x_{3}&=3.327243-\frac{\tan(3.327243) -\sin(3.327243)-2.75}{\sec^{2}(3.327243) -\cos(3.327243)}\\ &=4.505387\\ x_{3+1}=x_{4}&=4.505387-\frac{\tan(4.505387) -\sin(4.505387) -2.75}{\sec^{2}(4.505387)-\cos(4.505387)}\\ &=4.380159 \end{split} \end{equation*}$

These values, as of right now, are just values. We need to find their approximate errors to be able to tell if we are converging or not. We use the approximate relative error given by the formula:

$\begin{equation*} \varepsilon_{a}=\left| \frac{x_{n+1}-x_{n}}{x_{n+1}} \right| \times 100 \end{equation*}$

This gives us the percentage for the difference between our iterations. What should happen during these calculations is that we begin to see a trend of smaller and smaller errors which means the difference between subsequent calculations is less. This trend is how we can tell if we are converging to a root or not, using the Newton-Raphson method.

Example:

Using the values we found in the previous example compute the approximate relative error for each iteration.

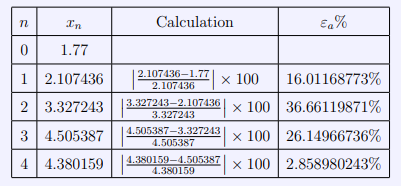
Here we can see that although the first few iterations created increasing error as we progressed through the iterations we began to narrow down to a root. We can see this because between the third and fourth iterations there was a drastic decrease in approximate relative error and the values for $x_{3}$ and $x_{4}$ are quite similar. Now we move to cover the Secant method for finding roots which is used in place of the Newton-Raphson method when a derivative is overtly challenging.

30.2 Secant Method

We previously stated that the Secant method is used when taking the derivative of a function would be too time consuming. This does not mean that the secant method does not still utilize $f'(x_{n})$ . In fact the secant method requires a formula in place of finding the actual derivative. The formula is given as follows.\index{Numerical Methods!Roots!Secant Method!Formula}

$\begin{equation*} f'(x_{n})=\frac{f(x_{n})-f(x_{n-1})}{x_{n} - x_{n-1}} \end{equation*}$

If we substitute this alternative into our original formula provided for the Newton-Raphson method we have the following.

$\begin{equation*} x_{n+1}=x_{n}-\left[ f(x_{n})\cdot \frac{x_{n} -x_{n-1}}{f(x_{n}) -f(x_{n-1})} \right] =x_{n} - \frac{f(x_{n})(x_{n}-x_{n-1})}{f(x_{n})-f(x_{n-1})} \end{equation*}$

Now that we have this formula we can compute an example to see how the Secant method is applied.

Example:

Given the equation $f(x)=x^{2}-20=0$ , apply the Secant method for three iterations. Then, compute the approximate relative error for each iteration [15].

We begin with assembling our formula for the Secant method as it applies to the given function.

$\begin{equation*} x_{n+1}=x_{n} - \frac{(x_{n}^{2} -20)(x_{n}-x_{n-1})}{(x_{n}^{2}-20)-(x_{n-1}^{2}-20)}=x_{n} - \frac{(x_{n}^{2} -20)(x_{n}-x_{n-1})}{x_{n}^{2}-x_{n-1}^{2}} \end{equation*}$

Now we were not given starting values for $n$ or $n-1$ . We need to compute them by first solving for $x$ in $f(x)=0$ .

$\begin{equation*} \begin{split} x^{2}-20=0 & \Rightarrow x^{2}=20\\ & \Rightarrow x=\pm \sqrt{20} \end{split} \end{equation*}$

From this we can let $x_{0}=4$ and $x_{1}=4.5$ since $4 < \sqrt{20} < 4.5$ . Now we can calculate the three iterations as follows.

$\begin{equation*} \begin{split} x_{1+1}=x_{2}&=4.5-\frac{((4.5)^{2} -20)(4.5-4)}{(4.5)^{2}-(4)^{2}}\\ &=4.470588\\ x_{2+1}=x_{3}&=4.470588-\frac{((4.470588)^{2} -20)(4.470588-4.5)}{(4.470588)^{2}-(4.5)^{2}}\\ &=4.472131\\ x_{3+1}=x_{4}&=4.472131-\frac{((4.472131)^{2} -20)(4.472131-4.470588)}{(4.472131)^{2}-(4.470588)^{2}}\\ &=4.472136 \end{split} \end{equation*}$

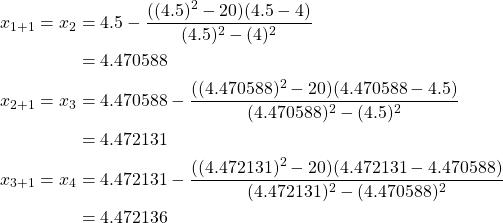
Next we calculate the approximate relative error for each iteration.

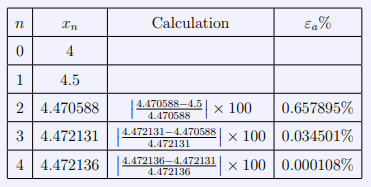
Here we can see some incredibly small errors and they continue to shrink which tells us that the iterations we are computing are quickly converging to the roots for the function $f(x)$ .

This concludes our exploration of approximating roots of nonlinear functions. In the next section we will cover solving differential equations using approximation methods.

36 Roots

License

Share This Book