Topology of R

Maggie Schildt

20 Topology of R

We have talked about the various ways to describe functions, sets, and relationships. In proofs we discussed being able to finesse the right amount of theorems and definitions to create a strong conclusion without throwing every possible relation in. This leads us to the definition of topology.

Definition. Topology

The study of geometric properties and spatial relations unaffected by the continuous change of shape or size of figures.

We can change a lot of what affects space, we are all familiar with the 3 sided fence problem in calculus where we are asked to find the lengths of the 3 sides against a barn to maximize the area of the pasture created. There are parts of this problem that never change like the minimum length of a side and the maximum length a side can be regardless of area. Topology is very similar in that it is the study of certain properties that cannot be changed by stretching or deforming, or twisting an object. The only restriction here is that we will only be addressing $\mathbb{R}$ . Lets begin with open and closed sets.

Open Sets

We have become very familiar with sets and we know that $\mathbb{R}$ contains many subsets. Open sets are one category of subsets for $\mathbb{R}$ . We give the following definition for open sets.

Definition.

A set $A\subset \mathbb{R}$ is open if, for every $x\in A$ , there is a $\epsilon>0$ such that $(x-\epsilon, x+\epsilon)\subseteq A$ . That is, if $|x-y|<\epsilon$ then $y\in A$ [18].

From this definition we can see that any element that is an element of an open set has an interval $(x-\epsilon, x+\epsilon)$ , which we call the $\epsilon$ -neighborhood of $x$ . The $\epsilon$ -neighborhood is the set of points inside the open set with a center of element $x$ and radius $\epsilon>0$ .

We will expand on neighborhoods a little later in this section but to summarize simply, an open set is a set with limit points that are not in the set. A great example, from a previous section, is the interval $(0,1)$ which Cantor proved to be uncountable. This means the set of real numbers on $(0,1)$ is an open set because the limit points 0 and 1 are not contained within the set.

Another category of open sets is the empty set $\emptyset$ . This is because the empty set contains no elements and therefor every element has a neighborhood in the empty set. The compliment to an open set is a closed set.

Closed Sets

Like when we discussed complement sets in set theory we can say that a closed set is the compliment to an open set and is defined as follows.

Definition.

A set $B\subset \mathbb{R}$ is closed if $B^{c}=\left\lbrace x\in \mathbb{R} :x\neq B\right\rbrace$ is open [18].

This truly does mean that a set is closed if the complimentary set is open. When we describe a closed interval we use “[]”, recall that for open sets we we used “()” on the interval. To provide an example of a closed set we consider the interval from 0 to 1 again, this time we have $[0,1]$ . In this case the set on the interval is closed because the indication is that 0 and 1 are both elements contained within the set.

We can think of open and closed sets like discontinuous and continuous functions. A discontinuous function has one or more points for which there is a skip in the function. This skip signifies an element that cannot work within the restrictions of the function and therefore there is no input or output for the function at that point, an example of a point is the value 0 for a denominator of a fraction which is simply impossible. When we think of open sets the elements of a set can get arbitrarily close to the end point but will never obtain the value of the end points just as 0 will never represent the value of a denominator for a fraction. Complementary to this we have closed sets which, like continuous functions, contain every element and for sets this means a closed set contains its end points.

Since this discussion of topology is for real numbers then it should be noted that empty sets, $\emptyset$ , and the set of real numbers $\mathbb{R}$ are the only sets that can be both open and closed.

Neighborhoods

We mentioned this idea of an $\epsilon$ -neighborhood when we gave the definition for an open set. looking back at that definition we saw that the $\epsilon$ -neighborhood was really an interval involving an element $x$ in the open set.

Most of the time a real analysis course will call a neighborhood for an open set an open ball. We call this an open ball because for each element $x$ in the open set we can create a ball of space in which that element $x$ is the center of the ball and $\epsilon>0$ is the radius. Furthermore the open set containing the neighborhoods for all points is also a neighborhood space. Lets try to put this in order a bit more.

Let $x$ be an arbitrary point $x\in S$ , $x$ an open set denoted $(x-\epsilon, x+\epsilon)$ . Now since $x$ is the center of this open set then we say this is the open neighborhood of point $x$ . Furthermore since set $S$ contains the open neighborhood for any arbitrary point $x$ then $S$ contains all open neighborhoods for all its points so $S$ is a neighborhood. Now that we have a strong understanding for open and closed sets and the neighborhood of open sets lets look at an example utilizing these properties for the intersection of sets.

Example:

Give an example of a countable collection of open sets

$\begin{equation*} \left\lbrace O_{1}, O_{2}, O_{3},...\right\rbrace \end{equation*}$

whose intersection $\int_{n=1}^{\infty}{O_{n}}$ is closed, not empty and not all of $\mathbb{R}$ [3].

Proof: Consider the example $O_{i}=\left\lbrace -\frac{1}{n}, \frac{1}{n}\right\rbrace$ for $n\in \mathbb{N}R$ . It can be observed that $\int_{n=1}^{\infty}{-\frac{1}{n}, \ \frac{1}{n}} = \left\lbrace 0 \right\rbrace$ because $O_{1}\supset O_{2}\supset O_{3}\supset...$ .

Now since $0\in O_{i}$ then there is $\epsilon >0$ such that for $N\leq n$ , $\frac{1}{n} \leq \frac{1}{N} < \epsilon$ . This means that there is no $\epsilon >0$ such that $\epsilon \in O_{i}$ therefore there can be no $\epsilon$ -neighborhood in $O_{i}$ so $\left\lbrace 0 \right\rbrace$ is closed and thus $\int_{n=1}^{\infty}{-\frac{1}{n}, \ \frac{1}{n}}$ is closed.

The Axiom of Completeness

The Completeness Axiom is a fundamental property of real numbers that later discussed properties for bounded sequences are derived from. We first introduce the idea of bounded sets as follows.

Definition. Upper Bound

A real number $a$ is called an upper bound for $S$ if $x\leq a$ for all $x\in S$ [17].

Definition. Lower Bound

A real number $b$ is called a lower bound for $S$ if $x\geq b$ for all $x\in S$ .

When a set has both an upper and a lower bound we say that the set is bounded. Now within upper and lowers bounds we have the least upper and greatest lower bounds defined as:

Definition.

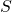Least Upper Bound(supremum): If $a$ is an upper bound for set $S$ then for every 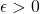$\epsilon >0$ there exists 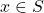$x\in S$ such that 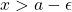$x>a-\epsilon$ . (There is no upper bound smaller than $a$ ) [17].
Greatest Lower Bound(infimum): If 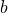$b$ is a lower bound for set 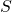$S$ then for every 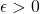$\epsilon >0$ there exists 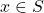$x\in S$ such that 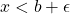$x< b+\epsilon$ . (There is no lower bound larger than $b$ )[17].

One might ask, what is the value in defining these terms when we already have maximum and minimum, the answer is that in analysis courses we have sets that do not have maximums or minimums and thus we introduce infimum and supremum to act in there place, since they are the least upper and greatest lower bounds and therefor do not always equate to a maximum or minimum respectively.

Example:

Let set $S=\left\lbrace 7,5,2,9,4,6\right\rbrace$ . Find the infimum and supremum.

Proof: We can see that $S$ is bounded above by 9 and below by 2. Let $\epsilon >0$ , then we have the intersection of the interval and set $S$ as $(9-\epsilon,9]\cap S$ thus we say $sup(S)=8$ . Let $\epsilon >0$ , then we have the intersection of the interval and set $S$ as $[2,2+\epsilon)\cap S$ and thus $inf(S)=1$ .

Now that we have a basic idea for upper and lower bounds let us now introduce the Completeness axiom [17].

Theorem: The Axiom of Completeness

Any nonempty subset of $\mathbb{R}$ that is bounded above has a least upper bound.

This theory is also true for lower bounded subsets and the greatest lower bound as well.

Heine-Borel Theorem

Beginning with the formal Heine-Borel theorem [17].

Theorem:

If a set $S$ of real numbers is closed and bounded, then the set $S$ is compact. [39]

This is a pretty easy to understand theorem and we can expand on it by explaining what compactness is. There is a more detailed way of describing the Heine-Borel theorem which is a space is considered compact if each open cover of $S$ has a finite subcover. We describe an open cover to be the collection or union of open sets of $S$ .

We put a lot of value in theorems such as the Heine-Borel theorem because compact spaces have a finite amount of properties. Since we study so much about the behavior of open sets having a subcategory, compact sets, takes us from an infinite list of possible properties and behaviors down to a finite amount of possible properties and behaviors. This allows us to prove and test, extensively, the properties for a space given that it is compact.

Let us continue the discussion of space and convergence in our next section on sequences. We will see a lot of the topology properties we discussed in terms of sets brought up again but this time for sequences.

20 Topology of R

License

Share This Book