Normal Force

Weight (also called force of gravity) is a pervasive force that acts at all times and must be counteracted to keep an object from falling. You definitely notice that you must support the weight of a heavy object by pushing up on it when you hold it stationary, as illustrated in Figure 1(a). But how do inanimate objects like a table support the weight of a mass placed on them, such as shown in Figure 1(b)? When the bag of dog food is placed on the table, the table actually sags slightly under the load. This would be noticeable if the load were placed on a card table, but even rigid objects deform when a force is applied to them. Unless the object is deformed beyond its limit, it will exert a restoring force much like a deformed spring (or trampoline or diving board). The greater the deformation, the greater the restoring force. So when the load is placed on the table, the table sags until the restoring force becomes as large as the weight of the load. At this point the net external force on the load is zero. That is the situation when the load is stationary on the table. The table sags quickly, and the sag is slight so we do not notice it. But it is similar to the sagging of a trampoline when you climb onto it.

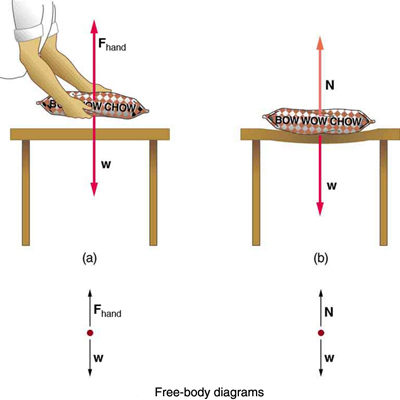
We must conclude that whatever supports a load, be it animate or not, must supply an upward force equal to the weight of the load, as we assumed in a few of the previous examples. If the force supporting a load is perpendicular to the surface of contact between the load and its support, this force is defined to be a normal force and here is given the symbol N. (This is not the unit for force N.) The word normal means perpendicular to a surface. The normal force can be less than the object’s weight if the object is on an incline, as you will see in the next example.

Tension

A tension is a force along the length of a medium, especially a force carried by a flexible medium, such as a rope or cable. The word “tension” comes from a Latin word meaning “to stretch.” Not coincidentally, the flexible cords that carry muscle forces to other parts of the body are called tendons. Any flexible connector, such as a string, rope, chain, wire, or cable, can exert pulls only parallel to its length; thus, a force carried by a flexible connector is a tension with direction parallel to the connector. It is important to understand that tension is a pull in a connector. In contrast, consider the phrase: “You can’t push a rope.” The tension force pulls outward along the two ends of a rope.

Consider a person holding a mass on a rope as shown in Figure 4.

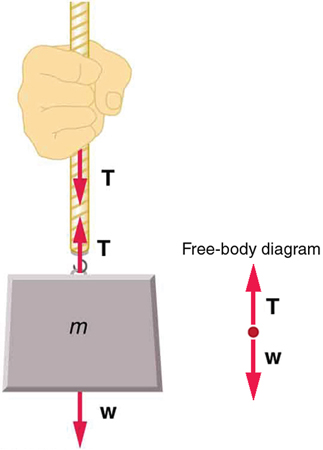
Tension in the rope must equal the weight of the supported mass, as we can prove using Newton’s second law. If the 5.00-kg mass in the figure is stationary, then its acceleration is zero, and thus F_net = 0. The only external forces acting on the mass are its weight w and the tension T supplied by the rope. Thus,

where T and w are the magnitudes of the tension and weight and their signs indicate direction, with up being positive here. Thus, just as you would expect, the tension equals the weight of the supported mass:

For a 5.00-kg mass, then (neglecting the mass of the rope) we see that

If we cut the rope and insert a spring, the spring would extend a length corresponding to a force of 49.0 N, providing a direct observation and measure of the tension force in the rope.

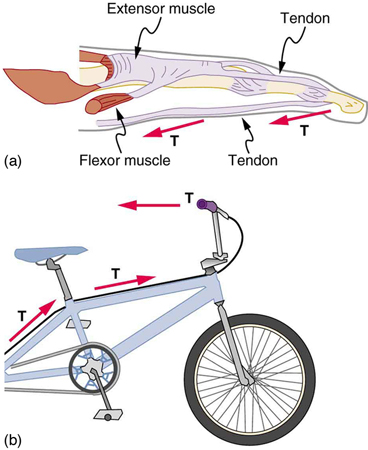
Flexible connectors are often used to transmit forces around corners, such as in a hospital traction system, a finger joint, or a bicycle brake cable. If there is no friction, the tension is transmitted undiminished. Only its direction changes, and it is always parallel to the flexible connector. This is illustrated in Figure 5 (a) and (b).

Extended Topic: Real Forces and Inertial Frames

There is another distinction among forces in addition to the types already mentioned. Some forces are real, whereas others are not. Real forces are those that have some physical origin, such as the gravitational pull. Contrastingly, fictitious forces are those that arise simply because an observer is in an accelerating frame of reference, such as one that rotates (like a merry-go-round) or undergoes linear acceleration (like a car slowing down). For example, if a satellite is heading due north above Earth’s northern hemisphere, then to an observer on Earth it will appear to experience a force to the west that has no physical origin. Of course, what is happening here is that Earth is rotating toward the east and moves east under the satellite. In Earth’s frame this looks like a westward force on the satellite, or it can be interpreted as a violation of Newton’s first law (the law of inertia). An inertial frame of reference is one in which all forces are real and, equivalently, one in which Newton’s laws have the simple forms given in this chapter.

Earth’s rotation is slow enough that Earth is nearly an inertial frame. You ordinarily must perform precise experiments to observe fictitious forces and the slight departures from Newton’s laws, such as the effect just described. On the large scale, such as for the rotation of weather systems and ocean currents, the effects can be easily observed.

The crucial factor in determining whether a frame of reference is inertial is whether it accelerates or rotates relative to a known inertial frame. Unless stated otherwise, all phenomena discussed in this text are considered in inertial frames.

All the forces discussed in this section are real forces, but there are a number of other real forces, such as lift and thrust, that are not discussed in this section. They are more specialized, and it is not necessary to discuss every type of force. It is natural, however, to ask where the basic simplicity we seek to find in physics is in the long list of forces. Are some more basic than others? Are some different manifestations of the same underlying force? The answer to both questions is yes, as will be seen in the next (extended) section and in the treatment of modern physics later in the text.

PHET EXPLORATIONS: FORCES IN 1 DIMENSION

Explore the forces at work when you try to push a filing cabinet. Create an applied force and see the resulting friction force and total force acting on the cabinet. Charts show the forces, position, velocity, and acceleration vs. time. View a free-body diagram of all the forces (including gravitational and normal forces).