5 The Structure of Crystalline Solids
Purpose
To investigate the structures of various commonly found motifs in crystalline structures.
Learning Outcomes
-
Define unit cell and describe how repeating unit cells lead to crystalline solids.
-
Be able to describe the structures of the following crystal structures: simple cubic, body-centered cubic, face-centered cubic, hexagonal close packing, and sodium chloride.
-
Define and determine the coordination numbers for crystalline solids.
-
Perform calculations relating the density and edge length for simple cubic, body-centered cubic, and face-centered cubic unit cells.
Textbook Reference
Tro, Chemistry – A Molecular Approach (5th Ed), Ch. 13.3 and 13.5.
Introduction
Many solids are found in regularly packed arrays of atoms, molecules, or ions. These are crystalline structures which form regularly packed structures and therefore are found to have distinctive, fixed structures . As a result, beautiful crystals of various elements and compounds can be found, such as that of sodium chloride and even proteins such as insulin can be observed. The presence of such structures imply that regular conformations of such elements or compounds can be found, and these can be measured using techniques such as X-ray diffraction.

The Unit Cell
A crystal structure is formed from a repeating array of identical units that are stacked in a repeating array. Each identical unit that can be stacked is referred to as a unit cell. Therefore, when classifying types of structures, what we typically do is to identify the structure of its unit cell.
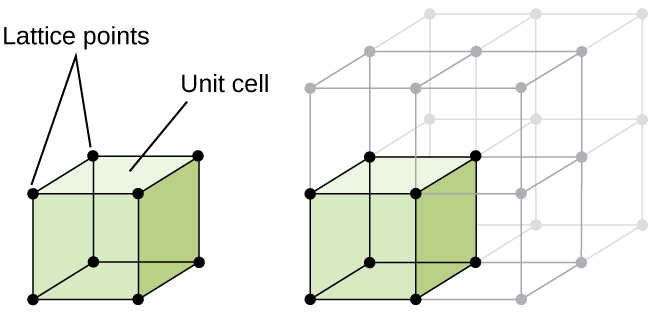
At the atomic level, a number of distinct common motifs for crystal structures can be observed. In this experiment, we will explore several common motifs for elemental crystal structures as well as the crystal structure of sodium chloride. We are also focusing on cubic unit cells.
Sharing Atoms Between Unit Cells
If we look at the face centered cubic unit cell, we will find that there is one atom at each corner, and one at the middle of each face.
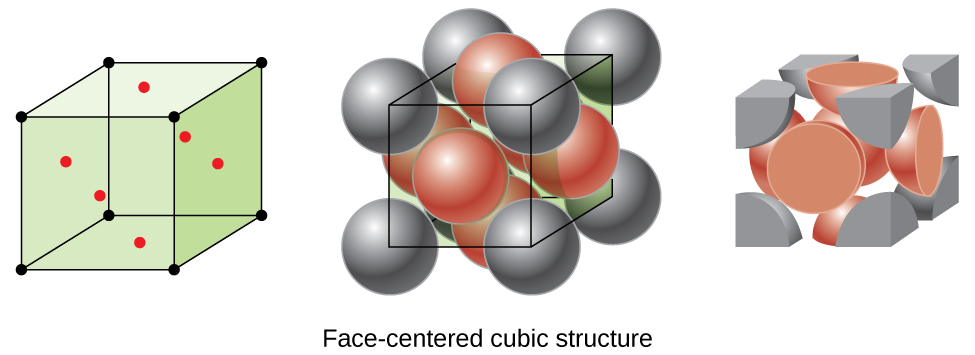
If you look at this unit cell, only half of the atoms on each face (the green atoms) are present within the center of the unit cell we’re talking about; the other half is in the adjacent unit cell. Similarly, only 1/8 of the unit cell at each corner is inside the central unit cell. This is summarized in the table below:
| Position | Proportion in a Unit Cell |
| center of unit cell/completely inside | 1 |
| on face of unit cell | 1/2 |
| on unit cell edge | 1/4 |
| at corner of unit cell | 1/8 |
The Menagerie of Unit Cells
Each crystal structure has a number of distinctive properties distinguishing it from other crystal structures; in turn, many of these properties are shared between substances with the same unit cell structure. One of these properties is the coordination number of a given atom.
Coordination Number
The coordination number of a particular species in a unit cell is the number of other atoms with which a particular atom of that species is in direct contact.
Example
A simple cubic unit cell has one atom at each corner of the unit cell. In this case, the atoms along each edge touch each other. Therefore, each atom is in direct contact with six different atoms (one on each side – up, down, front, back, left, right) and hence the coordination number is six.
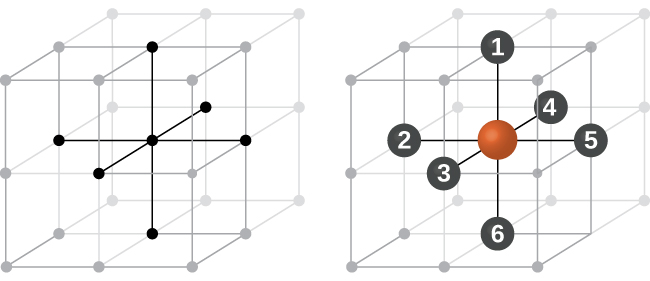
For fairly obvious reasons, for an ionic solid you would not expect ions with the same charge to be in direct contact with each other!
Visualization Exercise
In this exercise, you will study the crystal structures of a number of different (mostly metallic) elements as well as sodium chloride, an ionic solid. To do this, rather than trying to do this with paper-and-pencil type exercises or solid models, you will view a set of visualizations produced by Dean H. Johnstone at Otterbein College. Through viewing these structures, you will hopefully obtain a general understanding of a number of the main types of unit cell structures of crystalline solids.
Materials Studied
You will study a range of crystalline solid models as described below:
- Simple Cubic, such as polonium.
- Body-Centered Cubic, such as barium
- Face-Centered Cubic (or cubic closest packed), such as copper.
We will also study the crystalline structure of sodium chloride.
Procedures
Here, we outline how to complete the first part of the exercise with the simple cubic (Po) structure. The rest of the structures can be studied in a similar manner.
- Open the Crystals @ Otterbein crystal packing visualization.
- Under “Select Example”, click on “simple cubic (Po)”. A number of command buttons can be found on the right hand side, while in the middle you will see a depiction of the crystal structure for Polonium in a big square Jmol box.
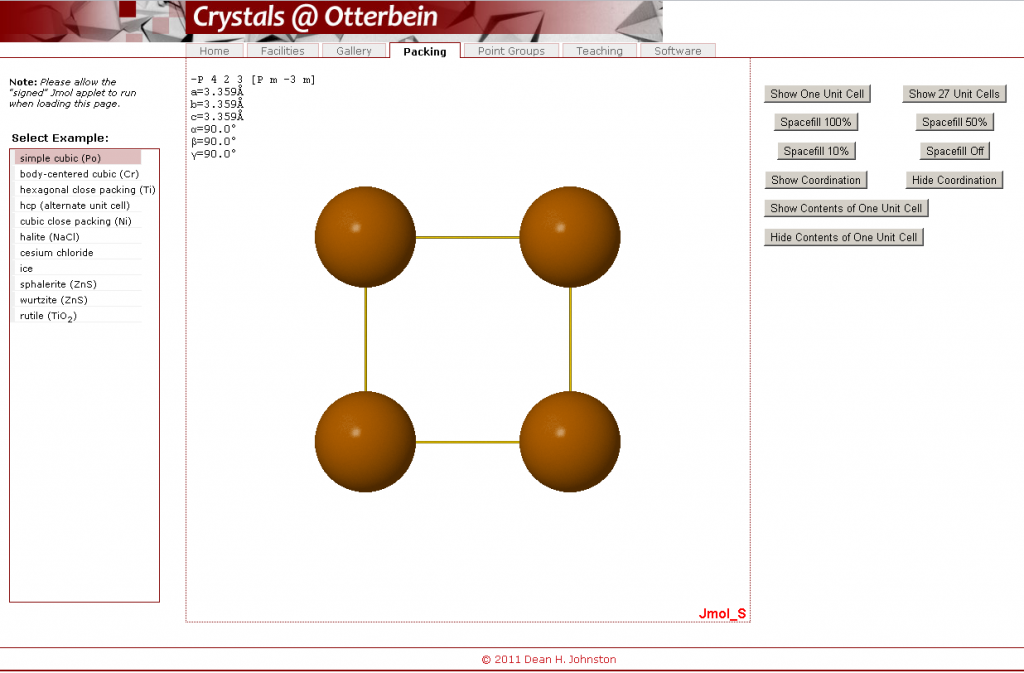
In this interface, several different actions can be completed. You are not required to perform any specific action; rather, these are actions that may help you from time to time, and you can choose to do whatever it takes to solve your problem.
- To rotate the molecule, click on the big square Jmol box containing the crystal structure and attempt to drag the molecule such that it rotates.
- To zoom in or out of the crystal structure, press on the shift button and, simultaneously, move the mouse up or down while clicking down on the structure. A number of additional functions are available through the menu you can access by right-clicking on the molecule.
- Show either a single unit cell or 27 unit cells (3 x 3 x 3) at once. Note that this shows all atoms as whole atoms even if only part of the atom is in each of these unit cells. In either case, it would help you determine the contents of the unit cells and how they, combined, form a crystal lattice.
- Change the proportion of the actual volume of the atoms that is taken up by the depicted spheres (e.g. “Spacefill 100%” means that the atoms take up the volume that they do in the ideal crystal structure (with atoms touching each other where appropriate). Note, however, that often you can see more detail with a 50% spacefill.
- You can choose whether you will see lines joining atoms that are touching each other by selecting “Show Coordination” or “Hide Coordination”. By counting these, you will be able to determine the coordination number for a given element by counting these links.
- When doing this, you must be careful to ensure that you are counting from a central atom (not on the edge of a unit cell); otherwise, you will undercount. Also, you will not be able to visualize this with a 100% spacefill setting
- “Show Contents of One Unit Cell” would show a single unit cell with only the parts of each atom that are actually inside the unit cell shown. This can be undone by “Hide Contents of One Unit Cell”.
- For some of the crystal structures, “Show layers” shows the closest parallel layers of atoms present in a given structure.
For a cubic unit cell, the proportion of an atom within a given unit cell is given above. from which the number of atoms in each unit cell can be determined. For this purpose, parts of different atoms can be added up to form a net of one (or more) atoms, as illustrated in the example below:
Examples
The ZnS (zincblende) crystal structure contains four zinc atoms completely inside each unit cell, while there are sulfur atoms at each corner and on each face of the unit cell:
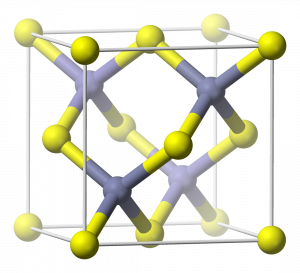
Therefore, in each unit cell, there are:
Using similar techniques, you will learn to describe the various unit cells in this experiment. Examine each of the unit cells that are studied in this experiment carefully, and answer the questions on the report form.
Calculations Involving Unit Cells
Given the structure of the unit cell, we can relate the following quantities through calculations:
- Density (which you can measure).
- Unit cell length (which can be determined using X-ray crystallography).
- Atomic radius.
For this section, we will focus only on cubic unit cells containing only one element, though the principles can be extended to more complex unit cells.
Relating the Density and Unit Cell Length
Given that we are focusing on cubic unit cells, the volume of a unit cell ![]() is related to the unit cell edge length
is related to the unit cell edge length ![]() by
by ![]() .
.
We can also, following the examples above, determine the number of atoms in a given unit cell.
Recalling that the density of any substance is given by
(1) ![]()
The mass of a unit cell can be found by determining the mass of the atoms within a unit cell, using Avogadro’s number as needed. As mentioned above, the volume and edge length can be related relatively easily.
Examples
Sodium has a density of 0.971 g/cm3 and is known to be in a unit cell where there are two atoms per unit cell. We can start by finding the volume of one unit cell:
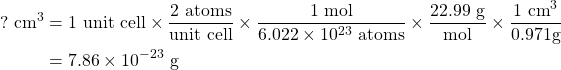
and then, by taking the cube root, we find that the edge length is
(2) ![]()
Relating the Edge Length and Atomic Radius
In this case, we need to recognize that for each unit cell, certain atoms can be deemed to be bordering each other, and hence a certain number of radii can be considered to be related to a characteristic length of the unit cell.
Example
For a simple cubic unit cell, atoms along the unit cell edge touch each other. As a result, the unit cell edge is two times that of the atomic radius. For example, since polonium has a unit cell edge length of 334 pm, the atomic radius is
(3) ![]()
