Purpose

• Measure different quantities and report the measurements using SI units.
• Familiarize yourself with the use of laboratory glassware and other measuring equipment.

Expected Learning Outcomes

• Report results of measurements and calculated values with the correct number of significant figures. (Lo 3)
• Calculate the percent error for a particular measurement. (LO 4)
• Use various pieces of glassware to measure the volume of a liquid sample. (LO 3)
• Determine the densities of liquid samples. (LO 3, 4)
• Compare the accuracy associated with using different glassware for measuring volume. (LO 4)

Textbook Reference

Tro, Chemistry: Structures and Properties, 2nd Ed, Chapter E.2, E.3, and E.5

Introduction

Significant Figures

When we make measurements and perform calculations, you can display a lot of digits (or add zeros incessantly). However, in reality you can only be certain of the answer to a particular level.

Therefore, it is necessary to express answers to reflect the degree to which you know a particular measurement. In Chemistry, the convention is that you know with certainty all digits that are marked on the measuring device. In addition, you can estimate, with some certainty, the quantity to an additional decimal place.  All of these are considered significant figures. What this means is that in chemistry, 11 mL, 11.0 mL and 11.00 mL are all different volumes that convey different information. 11 mL means the volume is within a few milliliters of 11 mL. It may or may not actually be 11 mL, but it’s definitely more than 6 mL and definitely less than 16 mL. 11.0 mL means that this volume is pretty close to being exactly 11 milliliters. It might be a few tenths of a milliliter off, but it’s pretty darn close. 11.00 mL means that for all practical purposes, this volume is exactly 11 milliliters. It might be off by a few hundreths of a milliliter, but for the purposes of this class, we can consider it to be exactly 11 milliliters.

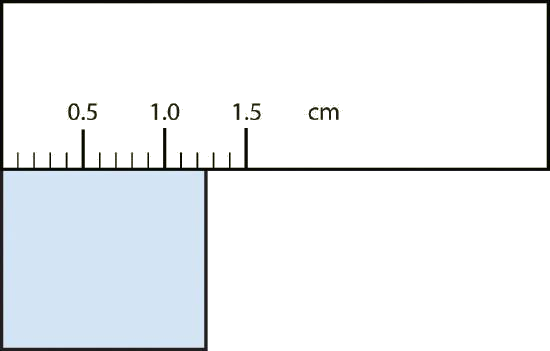
Measuring Volumes: Dealing with the Meniscus

For liquids in any container, there will typically be a curved surface rather than a flat surface.^[1] The meniscus needs to be read such that the the level of liquid read is the bottom of the meniscus (the curved surface).

One particularly important feature of a buret is that the graduations go downwards.  The 0 mL mark is at the top and the 50 mL mark is at the bottom.  This enables us to report the volume delivered as

 volume delivered = final volume – initial volume

Practically speaking, to determine if a digit is significant on a piece of glassware, figure out whether changing that digit by 5 would create a perceptible change in your glassware. If it does, then that digit is significant, if it doesn’t, then that digit is not significant.

Ex: If you are measuring out a liquid and find that the bottom of the meniscus is a bit above the 11 mL mark and you estimate that the actual volume is approximately 11.1 mL, but you’re not sure if you should write down 11.1 mL or 11.11 mL, ask yourself if you could distinguish the volume if you added a 5 to the last digit. Can you distinguish between 11.1 mL and 11.6 mL? If yes, then the tenths place is significant and you should ask yourself if you could distinguish between 11.11 mL and 11.16 mL. If yes, then the hundredths place is significant. If you don’t think you could distinguish between those two volumes with whatever piece of glassware you’re using, then the hundredths place is not significant.

Generally speaking, whether a digit is significant on a piece of glassware will be based on when the next graduation (marking) is on that piece of glassware. If the next graduation is for 12 mL, then you should be able to tell the difference between 11.1 and 11.6, but you wouldn’t be able to tell the difference between 11.11 and 11.16, thus you would write down 11.1 mL. But if the next graduation is for 20 mL (weird, I know, but it’s hypothetical), then you would not be able to tell the difference between 11.1 and 11.6, so you would just write down 11 mL. But if there are graduations every 0.1 mL and you see that the meniscus is just above the 11.1 mL mark and well below the 11.2 mL mark, then you would definitely be able to tell the difference between 11.1 mL and 11.16 mL, thus you would write down 11.11 mL.

Accuracy and Precision

We use accuracy and precision to characterize the quality of measurements.  It is important to realize that it is impossible to measure anything completely accurately or precisely; however, especially in analytical chemistry, it is very important that we try our best to be as accurate and precise as possible.

Accuracy

Accuracy refers to how close measurements compare to the true (accepted) value. To do this, we measure a quantity for which we know the accepted value. A common measure of the accuracy of the measurement is given by the percent error:^[2]

[latex]\text{% error} = \frac{\text{measured value} - \text{true value}}{\text{true value}} \times 100\%[/latex]

Note that the percent error can be positive or negative. In this course, the sign for the percent error is often kept to indicate the possible direction of any systematic error.^[3]

Precision

Precision refers to how close a set of measured results are to each other. A numerical measure of the precision of a measurement is given by its standard deviation, which, for a sample containing n values [latex]x_1, x_2, \cdots, x_n[/latex], is given by

[latex]s = \sqrt{\frac{\sum\limits_{i=1}^{n} (x_i - \bar{x})^2}{n-1}}[/latex]

where [latex]\bar{x}[/latex] is the mean. The larger the standard deviation, the lower the precision. This is often easily calculated by typing in the numbers into Excel and having Excel solve for the standard deviation using the STDEV function by typing “=stdev([select relevant data])” into excel. Note that you can also use =stdev.s() if you want, but do NOT use =stdev.p().

Density

The density of a particular homogeneous substance (pure substance or mixture) is the mass per unit volume.

[latex]\mbox{density} = \frac{\mbox{mass}}{\mbox{volume}}[/latex]

In many cases, for liquids, the density is measured in grams per milliliter (g/mL). In this case, the mass is measured in grams and the volume is measured in milliliters. An identical unit (more commonly used for solids) is grams per cubic centimeter} [latex]\left(\frac{\mbox{g}}{\mbox{cm}^3}\right)[/latex]. For gases, grams per liter (g/L) is more commonly used.

Density is an intensive property – it doesn’t depend on the amount of substance present. Therefore, we will get the same value if we measure the density of teaspoon of water or a tanker truck full of water.

Procedures

Special Equipment Needed

The following equipment will be needed:

• 50/100 mL beaker.
• Three 100 mL graduated cylinders.
• buret
• 10 mL volumetric pipet
• P1000 micropipettors and tips

The idea here is to measure out a certain volume of deionized water using different instruments and determine its mass. From this information, we will be able to determine the density of water measured using the different instruments. This means that any time you record a volume of water in this lab, you should be recording what the piece of glassware you’re using to measure the volume says the volume is to the correct number of significant figures. Do NOT use the mass of the water to calculate the volume.

Determining the Temperature of Water

In this part, you will determine the temperature of water.  From this, you will be able to look up the exact density of water from tables like this.

1. Fill a 400 or 600 mL beaker with approximately 300 mL of deionized water, and determine the temperature of this water.
   1. The volume here is just approximate.  We aren’t even measuring
   2. Also, it may be easier to get this straight from the deionized water tap rather than from the wash-bottle.

Using a Medicine Dropper to Measure the Volume of Water

A useful rule of thumb is that 20 drops from a medicine dropper is about 1 mL. To determine if this is a good rule of thumb, we will determine the mass of 20 drops of water.

2. Obtain an empty, dry 50 or 100 mL small beaker and determine its mass.
3. Using a medicine dropper, place 40 drops of deionized water into this beaker and determine the combined mass of the water and the beaker.  Calculate the volume of the water assuming that 20 drops is exactly 1 mL.
4. Empty and dry the beaker with a paper towel.
5. Repeat steps 2-4 two more times.

Measuring the Volume of Water Using a 50 mL Beaker

6. Check to make sure there are graduations on the beaker. If not, get another beaker.
7. Determine the mass of the empty, dry 50 mL beaker.
8. Measure out about 20 mL of deionized water using the beaker. Estimate the volume of this water to the correct number of significant figures.

9. Ensure that the outside of the beaker is completely dry, and determine the mass of the beaker containing this water.
10. Empty and dry the beaker with a paper towel.
11. Repeat steps 7-10 two more times.

Measuring the Volume of Water Using a 50 mL Graduated Cylinder

12. Accurately weigh a clean, dry 50 mL graduated cylinder.
13. Fill the graduated cylinder up to the 20 mL mark with deionized water, using a disposable pipet to get the volume as close as possible to exactly 20 mL (but don’t worry if it’s not perfect). Report the actual volume of the water to the appropriate number of significant figures. Hint: the last digit you report should NOT be 0 unless you are one of the rare people who was able to measure out exactly 20 mL.
14. Weigh the graduated cylinder containing the water.
15. Empty the graduated cylinder, and shake out all excess water. Make sure no beads of water remain.
16. Repeat steps 12 to 15 two more times.

Measuring the Volume of Water Using a Buret

17. Rinse the buret 2-3 times with a 10 mL portion of deionized water. You may wish to hold the buret approximately horizontally and then rotate the buret to do this. Try and ensure that there are no water droplets on the walls of the buret.
18. Clamp the buret to a stand using a buret clamp. Ensure that the buret is completely vertical (walk around the buret and observe it from all sides to ensure it is vertical) and held in place in the clamp. Seek help from your instructor if you have difficulties.
19. Fill the buret to approximately the 10 mL mark and release water into a waste beaker until all air bubbles are removed from the buret.
20. Determine the mass of a clean, dry 50 or 100 mL beaker.
21. Record the liquid level on the buret at this time; this is the initial volume. Make sure that this is recorded to the correct number of significant figures.
22. Place the dry 50 or 100 mL beaker under the buret and open the stopcock and allow a bit more than 10.00 mL of water to flow through (use the buret to measure this volume, NOT the beaker). Record the volume of the buret at this point to the correct number of significant figures; this is the final volume. Hint: the final volume you record should be a bit more than 10 mL greater than the initial volume you recorded.
23. Wipe the outside of the beaker to ensure it is dry and measure the mass of the beaker and the water.
24. Empty and dry the beaker with a paper towel.
25. Repeat steps 20-24 two more times. If you have insufficient water in the buret for the next addition, then you will need to refill the buret; however, if there is sufficient water already present, you can just start from the water already present in the buret.

Measuring the Volume of Water Using a Volumetric Pipet

26. Obtain about 40-45 mL of deionized water and put this in a clean, dry 100 mL (or larger) beaker or Erlenmeyer flask.
27. Half-fill the pipet with deionized water and rinse the pipet by holding it horizontally and rotating it, similar to how you rinsed the buret earlier in step 17.
28. Determine the mass of a clean, dry 50 or 100 mL beaker.
29. Pipet 10.00 mL of deionized water and dispense this into the small beaker that you weighed earlier (remember touch the tip of the pipet to the wall of the beaker while dispensing the water, but do NOT to expel the last bit of liquid stuck in the tip of the pipet). Record the volume as 10.00 mL – volumetric pipets typically are accurate to four significant figures^[5]
30. Determine the mass of the beaker containing water delivered by the pipet.
31. Empty and towel-dry the beaker.
32. Repeat steps 28-31 two more times.

Measuring the Volume of Water Using a Micropipettor

33. Obtain about 40-45 mL of deionized water and put this in a clean, dry 100 mL (or larger) beaker or Erlenmeyer flask.
34. Obtain a P1000 micropipettor and place a pipette tip on the bottom as demonstrated by your instructor.
35. Set the pipettor to 1000 by twisting the top.  This will set the measurement to be at 1000 μL = 1 mL.
36. Determine the mass of a clean, dry 50 or 100 mL beaker.
37. Pipette 10 mL of deionized water into the clean, dry 50 or 100 mL beaker from the previous step by using the P1000 micropipettor to transfer ten 1.000 mL aliquots of deionized water from the 100 mL (or greater) beaker/Erlenmeyer flask used in step 33.  Record the volume as 10.000 mL -this is how P1000 micropipettors are typically graduated (to the nearest 0.005 mL).
38. Determine the mass of the beaker containing water delivered by the micropipettor.
39. Empty and towel-dry the beaker.
40. Repeat steps 33-39 two more times.

Acknowledgment

This experiment is based on similar experiments for CHEM 105 and CHEM 120L at Fort Hays State University.