4 Applications
We have only looked at a few main ideas of calculus so far, and there are already many applications we can discuss. We will mention a few of the applications of derivatives and integrals and then discuss a couple applications in depth. The following applications come from Larson and Edwards [15].
Applications of Derivatives
Find velocity and acceleration
Find the rate of change
- Bacteria growth
- Depreciation
Find related rates
- Speed of a plane
- Velocity change of piston
Find path of a projectile
Optimize and minimize
- Optimize profit
- Minimize cost, time,
or distance
Estimate error
Sketch curves
Applications of Integrals
Find area, surface area,
and volume
Find arc length
Find work done by a changing force
Find centers of mass
Find fluid force exerted on submerged object
The first application that we will take a look at is related rates. Related rates are important and can be applied to a variety of scenarios. From finding how fast the water level is rising in a tank to determining the speed of planes, related rates can be applied to really any scenario where one rate is dependent on another. Related rates can even save lives as we will see in our example.
The second application we will be discussing is that of work, specifically the work done by a varying force. Work is important because it is the amount of energy needed to perform different tasks [15]. For example, it is necessary to know how much energy is needed to compress a spring to make a garage door open and close properly or how much energy is needed to send a rocket into space [15]. Without forces and energy, the world would not be able run and would not even exist. Because forces and energy are such an integral part of the physical world, the importance of being able to calculate work cannot be overstated.
Related Rates
The problem we will be solving has to do with the distance between two planes that are traveling at constant speeds and comes from Larson and Edwards [15]. This is a related rates problem because the rate at which the distance between the two planes is changing over time is dependent on the rates at which each plane is moving. Additionally, we will need to use implicit differentiation (see Part I: Chapter 2) as we work through this problem that I completed for Calculus I.
An air traffic controller spots two planes at the same altitude converging on a point as they fly at right angles to each other. One plane is 225 miles from the point moving at 450 miles per hour. The other plane is 300 miles from the point moving at 600 miles per hour. At what rate is the distance between the planes decreasing? How much time does the air traffic controller have to get one of the planes on a different flight path? The image below provides a visual representation of this problem and is taken from Larson and Edwards [15].
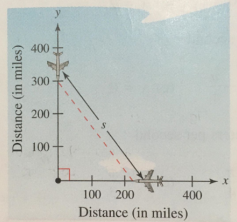
Solution
Let ![]() be the number of miles of the first plane from the point of convergence,
be the number of miles of the first plane from the point of convergence, ![]() be the number of miles of the second plane from the point of convergence,
be the number of miles of the second plane from the point of convergence, ![]() be the number of miles between the two planes, and
be the number of miles between the two planes, and ![]() be the time in hours. From the information given in the problem, we have
be the time in hours. From the information given in the problem, we have
![]()
At the time the air traffic controller spotted the two planes,
![]()
By the Pythagorean Theorem,
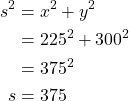
What we want to find is ![]() , which is the rate at which the distance between the planes is decreasing with respect to time. By the Pythagorean theorem,
, which is the rate at which the distance between the planes is decreasing with respect to time. By the Pythagorean theorem,
![Rendered by QuickLaTeX.com \begin{align*} s^2&=x^2+y^2 \\ \frac{d}{dt}[s^2]&=\frac{d}{dt}[x^2]+\frac{d}{dt}[y^2] &&\text{Differentiate w.r.t $t$}\\ \frac{d}{dt}[h(t)^2]&=\frac{d}{dt}[g(t)^2]+\frac{d}{dt}[f(t)^2] \\ 2h(t)\cdot\frac{d}{dt}h(t)&=2g(t)\cdot\frac{d}{dt}g(t)+2f(t)\cdot\frac{d}{dt}f(t) &&\text{Chain Rule}\\ 2s\frac{ds}{dt}&=2x\frac{dx}{dt}+2y\frac{dy}{dt} \\ 2(375)\frac{ds}{dt}&=2(225)(-450)+2(300)(-600) &&\text{Substitute}\\ \frac{ds}{dt}&=\frac{-202,500-360,000}{750}\\ &=-750 \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4250086936d16e8dfc15b62e53b86f1f_l3.png)
Therefore, the distance between the two planes is decreasing at a rate of 750 miles per hour.
We now want to know how much time will pass before the planes collide. That is, at what time ![]() will the distance between the planes be 0? We have that
will the distance between the planes be 0? We have that
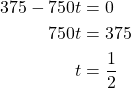
Therefore, the air traffic controller has half an hour to get one of the planes on a different flight path.
Calculating Work
There are many different types of problems we could do related to calculating work, but the one we are going to do is finding how much energy is needed to compress springs in a garage door. That is, we are going to find the work done by the springs.
However, before we begin, we need to introduce a couple of formulas. The following definition and law are stated by Larson and Edwards as follows [15].
If an object is moved along a straight line by a continuously varying force
![]()
is given by
![]()
The force
![]()
where the constant of proportionality ![]() (the spring constant) depends on the specific nature of the spring.
(the spring constant) depends on the specific nature of the spring.
Now we are ready to begin our problem which I completed for Calculus I and comes from Larson and Edwards [15].
An overhead garage door has two springs, one on each side of the door. A force of 15 pounds is required to stretch each spring 1 foot. Because of the pulley system, the springs stretch only one-half the distance the door travels. The door moves a total of 8 feet, and the springs are at their natural length when the door is open. Find the work done by the pair of springs.
Solution
By Hooke’s Law,
![]()
where ![]() is the distance a spring is stretched or compressed from its original length. We are given that it takes a force of 15 pounds to stretch each spring one foot. So we have,
is the distance a spring is stretched or compressed from its original length. We are given that it takes a force of 15 pounds to stretch each spring one foot. So we have,
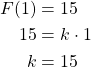
Therefore,
![]()
We are also given that the springs are at their natural length when the door is open and stretch four feet when the door is closed.Now to find the work done by ![]() we need to integrate. By definition I.10,
we need to integrate. By definition I.10,

Thus, 120 foot-pounds are needed to stretch one spring. Therefore, the total work done by both springs is 240 foot-pounds.
Up to this point, we have only been dealing with functions of one independent variable. However, when dealing with the real world, it is unlikely that the problems encountered will be affected by only one variable. This is why we are now going to discuss multivariate calculus.
