15 Functions
We have already seen and worked with functions previously in the Calculus section, but we have never defined what a function is. A function is a special type of relation where for each ![]() in the domain there exists one and only one
in the domain there exists one and only one ![]() in the range that
in the range that ![]() is related to, which is stated in the second part of the following formal definition from Smith et al. [23].
is related to, which is stated in the second part of the following formal definition from Smith et al. [23].
A function (or mapping) from
- the domain of
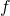 is
is  and
and - if
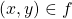 and
and 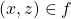 , then
, then 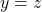 .
.
There is more notation and terminology related to functions that Smith et al. provides. ![]() means that “
means that “![]() is a function from
is a function from ![]() to
to ![]() ” or “
” or “![]() maps
maps ![]() to
to ![]() .” The codomain of
.” The codomain of ![]() is
is ![]() , and
, and ![]() is a function on
is a function on ![]() if
if ![]() .
. ![]() means that
means that ![]() is an element of
is an element of ![]() .
. ![]() is the image or value of
is the image or value of ![]() at
at ![]() , and
, and ![]() is the pre-image of
is the pre-image of ![]() [23].
[23].
One more thing to note is that the range and codomain are not necessarily equal sets. The range is the set of all ![]() -values such that
-values such that ![]() for some
for some ![]() in the domain. The codomain includes all of the range values but may also include values that are not mapped to from some
in the domain. The codomain includes all of the range values but may also include values that are not mapped to from some ![]() in the domain. For example, we can define a function
in the domain. For example, we can define a function
![]()
![]()
The codomain is ![]() , but the range is much smaller. For instance, the negative rational numbers are all elements of the codomain but are not elements of the range.
, but the range is much smaller. For instance, the negative rational numbers are all elements of the codomain but are not elements of the range.
The range is always a subset of but is not necessarily equal to the codomain. Later on, we will discuss a special type of function where the range and codomain are equal sets.
Let’s go through an example of how to determine whether a relation is a function. This is a problem that I completed for Calculus I that comes from Larson and Edwards [15].
Determine whether
Solution
Suppose that ![]() and
and ![]() are elements of
are elements of ![]() . According to the definition of a function,
. According to the definition of a function, ![]() must equal
must equal ![]() . So, if we show that
. So, if we show that ![]() , we will have proven that
, we will have proven that ![]() is a function. We have
is a function. We have
![]()
Thus, we have that ![]() and
and ![]() are elements of
are elements of ![]() . However, because
. However, because
![]()
![]() . Therefore,
. Therefore, ![]() is not a function by Definition III.6.
is not a function by Definition III.6.
Just as we have different types of relations, we also have different types of functions. These types are one-to-one and onto.
One-to-one
A function is one-to-one if the elements of the domain have a one-to-one correspondence to the elements of the range. When we defined a function, we said that a relation was a function if each value in the domain mapped to one and only one value in the range. That is, if ![]() and
and ![]() , then
, then ![]() . However, a function does not place any restrictions on how many domain values can map to a single range value. A one-to-one function then is one where each range value is mapped to from one and only one domain value. This can be visualized as follows:
. However, a function does not place any restrictions on how many domain values can map to a single range value. A one-to-one function then is one where each range value is mapped to from one and only one domain value. This can be visualized as follows:

The above diagram is that of the function ![]() . The ellipse on the left is the domain, and the one on the right is the codomain. Notice how the elements of the domain have a one-to-one correspondence with the elements of the range. There is not a single point that has two lines coming from it.
. The ellipse on the left is the domain, and the one on the right is the codomain. Notice how the elements of the domain have a one-to-one correspondence with the elements of the range. There is not a single point that has two lines coming from it.
Now that we have an idea of what a one-to-one function is, let’s look at the following formal definition provided by Smith et al. [23].
A function
So, how do we determine whether a function is one-to-one? According to Smith et al., we could do a direct proof by assuming that ![]() and then showing that
and then showing that ![]() , or we can prove the contrapositive by assuming
, or we can prove the contrapositive by assuming ![]() and then showing that
and then showing that ![]() [23]. Let’s practice using a homework problem from Smith et al. that I completed for this paper [23].
[23]. Let’s practice using a homework problem from Smith et al. that I completed for this paper [23].
Prove that the function
![]()
is one-to-one.
Proof.
We need to show for all ![]() where
where ![]() that if
that if ![]() , then
, then ![]() . Using the direct proof method, suppose that
. Using the direct proof method, suppose that ![]() , then
, then
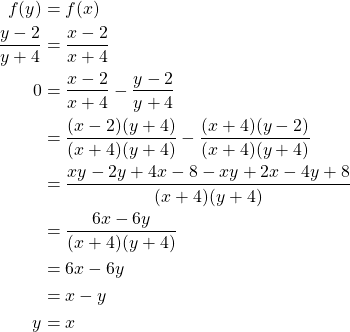
Since ![]() , we need to show that
, we need to show that ![]() for all
for all ![]() . We will prove this by contradiction. Suppose that
. We will prove this by contradiction. Suppose that ![]() for some
for some ![]() .
.
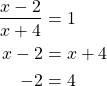
Since ![]() , we have reached a contradiction and have proven that
, we have reached a contradiction and have proven that ![]() for all
for all ![]() Thus,
Thus, ![]() if and only if
if and only if ![]() . Therefore,
. Therefore, ![]() is a one-to-one function.
is a one-to-one function.
Onto
A function is onto if the domain maps onto the entire codomain. That is, for each element in the codomain, there exists at least one element in the domain that maps to it. This can be visualized as follows:
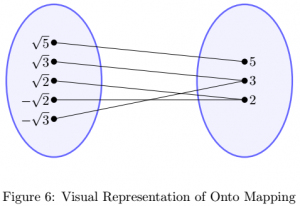
The above diagram is that of the function ![]() . The ellipse on the left is the domain, and the one on the right is the codomain. Notice how the elements of the codomain each have an element of the domain that maps to it. Let’s now look at the formal definition provided by Smith et al. [23].
. The ellipse on the left is the domain, and the one on the right is the codomain. Notice how the elements of the codomain each have an element of the domain that maps to it. Let’s now look at the formal definition provided by Smith et al. [23].
A function
So, how do we go about showing that the range is equal to the codomain? Recall from chapter 13, that two sets are equal if each is a subset of the other. Since we already know that the range is a subset of the codomain, all we have to show is that the codomain is a subset of the range. That is, we show that if ![]() is an element of the codomain then
is an element of the codomain then ![]() must be an element of the range. Let’s practice with a homework problem from Smith et al. that I completed for this paper [23].
must be an element of the range. Let’s practice with a homework problem from Smith et al. that I completed for this paper [23].
Prove that the function
![]()
is onto.
Proof.
We need to show that every element in the codomain is an element of the range by showing that there exists an ![]() such that
such that ![]() for all
for all ![]() . We have that
. We have that
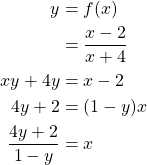
Since ![]() is a real number for all real numbers
is a real number for all real numbers ![]() except
except ![]() , we can find a real number
, we can find a real number ![]() such that
such that ![]() for all
for all ![]() in the codomain except for
in the codomain except for ![]() . But based on how the function is defined,
. But based on how the function is defined, ![]() . Since for all
. Since for all ![]() in the codomain there exists an
in the codomain there exists an ![]() in the domain such that
in the domain such that ![]() , every element in the codomain is also in the range. Thus, the codomain is a subset of the range, and the range and codomain are equal. Therefore, the function is onto.
, every element in the codomain is also in the range. Thus, the codomain is a subset of the range, and the range and codomain are equal. Therefore, the function is onto.
Not only is it possible for a function to be one-to-one or onto, but it is also possible for a function to be both. In fact, functions that possess both of these characteristics are at the center of what it means for two sets to be equivalent, which in turn lays the foundation for our next topic, cardinality.
