19 Topology of the Real Numbers
The foundation for the discussion of the topology of ![]() is the Axiom of Completeness. However, before we discuss this axiom, we must be introduced to a couple more terms, the upper bound and least upper bound of a set. Abbott provides us with the following definition [1].
is the Axiom of Completeness. However, before we discuss this axiom, we must be introduced to a couple more terms, the upper bound and least upper bound of a set. Abbott provides us with the following definition [1].
A set
An upper bound of a set ![]() in the real numbers is simply a real number that is greater than or equal to every element in
in the real numbers is simply a real number that is greater than or equal to every element in ![]() . An upper bound is not required to be an element of
. An upper bound is not required to be an element of ![]() , and it is possible for a set to have an infinite number of upper bounds. However, there is one upper bound in particular that we are usually interested in. This brings us to our next definition presented by Abbott [1].
, and it is possible for a set to have an infinite number of upper bounds. However, there is one upper bound in particular that we are usually interested in. This brings us to our next definition presented by Abbott [1].
A real number
 is an upper bound for
is an upper bound for  .
.- If
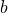 is an upper bound for
is an upper bound for  , then
, then 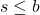 .
.
So, the least upper bound of a set ![]() , denoted as sup
, denoted as sup ![]() , is simply the smallest upper bound that exists. Now that we have defined these ideas, we are ready for the Axiom of Completeness.
, is simply the smallest upper bound that exists. Now that we have defined these ideas, we are ready for the Axiom of Completeness.
Axiom of Completeness
The real numbers are the foundation on which we build the branch of mathematics known as analysis, and the Axiom of Completeness is what enables us to construct the set of real numbers from the set of rationals [1]. The defining difference between these two sets is that ![]() is not filled with gaps like
is not filled with gaps like ![]() is, and this axiom is the formal statement of this difference [1]. Abbott gives the following statement of this axiom [1].
is, and this axiom is the formal statement of this difference [1]. Abbott gives the following statement of this axiom [1].
Axiom of Completeness. Every nonempty set of real numbers that is bounded above has a least upper bound.
This in itself does not seem very interesting. In fact, what this axiom is saying seems quite obvious. What is interesting, however, is why this axiom does not hold true for the rationals.
To explain this, Abbott uses the example of the set ![]() defined as
defined as
![]()
The least upper bound of ![]() is
is ![]() when we are not restricted to the rationals because
when we are not restricted to the rationals because ![]() is an irrational number [1]. If we are restricted to the rationals, then the obvious choice for the least upper bound would be the smallest rational number greater than
is an irrational number [1]. If we are restricted to the rationals, then the obvious choice for the least upper bound would be the smallest rational number greater than ![]() . The problem is that between any two real numbers, there exists a rational number, which is formally stated in Theorem IV.4. Whenever we think we have found the smallest rational greater than
. The problem is that between any two real numbers, there exists a rational number, which is formally stated in Theorem IV.4. Whenever we think we have found the smallest rational greater than ![]() , we have not because there is another rational between this supposed smallest and
, we have not because there is another rational between this supposed smallest and ![]() . Thus, it is impossible to find a least upper bound when restricted to the rational numbers.
. Thus, it is impossible to find a least upper bound when restricted to the rational numbers.
Let’s now look at an example that demonstrates how the Axiom of Completeness can be used in proving statements. The following example is a homework problem I completed for Introduction to Analysis and comes from Abbott [1].
Example 39
Let ![]() be nonempty and bounded above, and let
be nonempty and bounded above, and let ![]() have the property that for all
have the property that for all ![]() ,
, ![]() is an upper bound for
is an upper bound for ![]() and
and ![]() is not an upper bound for
is not an upper bound for ![]() . Show
. Show ![]() .
.
Proof.
By the Axiom of Completeness, the least upper bound of ![]() exists. For all
exists. For all ![]() ,
, ![]() cannot be the least upper bound because
cannot be the least upper bound because ![]() is a smaller upper bound. We are also given that
is a smaller upper bound. We are also given that ![]() is not an upper bound for all
is not an upper bound for all ![]() . Thus, the least upper bound
. Thus, the least upper bound ![]() satisfies
satisfies ![]() for all
for all ![]() . Therefore,
. Therefore, ![]() must equal
must equal ![]() , and
, and ![]() .
.
In this proof, we needed to show that the supremum (least upper bound) of ![]() actually existed before we could show what value the supremum was equal to. The Axiom of Completeness was very important in that it guaranteed the existence of the supremum of
actually existed before we could show what value the supremum was equal to. The Axiom of Completeness was very important in that it guaranteed the existence of the supremum of ![]() .
.
Using the Axiom of Completeness, we have another interesting result which is given by Abbott in the following theorem [1].
Theorem IV.4 (Density of ![]() in
in ![]() )
)
This theorem then enables us to prove the following corollary given by Abbott [1]. The proof is a homework problem I completed for Introduction to Analysis.
Corollary IV.4.1 (Density of ![]() in
in ![]() )
)
Proof.
Let ![]() such that
such that ![]() . Because
. Because ![]() and
and ![]() is closed under addition,
is closed under addition, ![]() . Since
. Since ![]() and
and ![]() is an ordered field,
is an ordered field,
![]()
By Theorem IV.4, there exists ![]() such that
such that
![]()
By Example 24 in chapter 11, ![]() since
since ![]() and
and ![]() . Therefore, given any two real numbers
. Therefore, given any two real numbers ![]() and
and ![]() where
where ![]() , there exists an irrational number
, there exists an irrational number ![]() satisfying
satisfying ![]() .
.
The density of ![]() and
and ![]() in
in ![]() is amazing. No matter how small the distance between two real numbers, we can always find both a rational and irrational between them. This is just incredible. But we still have much more to discuss relating to the topology of
is amazing. No matter how small the distance between two real numbers, we can always find both a rational and irrational between them. This is just incredible. But we still have much more to discuss relating to the topology of ![]() so we should move on to our next interesting concepts, those of open and closed sets.
so we should move on to our next interesting concepts, those of open and closed sets.
Open and Closed Sets
When discussing open and closed sets, we must be careful not to think of them in terms of the traditional meanings of open and closed. Normally, we think that when something is not open that it must be closed and vice versa. But it is possible for a set to be open, closed, neither, or both. It may also be tempting to think that a closed set is bounded and an open set is not, but that would also be incorrect thinking.
Before we get into the definitions of open and closed, we must understand a couple more ideas, epsilon neighborhoods and limit points. Abbott provides us with the following formal definitions [1].
Given a real number
![]()
is called the epsilon neighborhood (![]() -neighborhood) of
-neighborhood) of ![]() .
.
In other words, the ![]() -neighborhood of a real number
-neighborhood of a real number ![]() is the set of all real numbers whose distance from
is the set of all real numbers whose distance from ![]() is less than
is less than ![]() .
.
A point
A limit point of a set is not necessarily an element of the set. But if ![]() is a limit point of
is a limit point of ![]() , then at least one of the following must be true.
, then at least one of the following must be true.
- For all
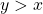 , either
, either 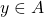 or
or 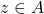 such that
such that 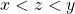 .
. - For all
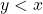 , either
, either 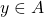 or
or 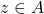 such that
such that 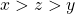 .
.
Now we are ready to introduce the definitions of open and closed sets as given by Abbott [1].
A set
In other words, a set ![]() is open if and only if for every element
is open if and only if for every element ![]() in
in ![]() we can find
we can find ![]() and
and ![]() in
in ![]() such that
such that ![]() , and
, and ![]() .
.
A set
As mentioned previously, a limit point of a set is not necessarily an element of the set. However, if every limit point is an element, then the set is closed.
Let’s now look at a couple of examples that I wrote and completed for this paper to better understand these concepts.
Example 40
Determine whether ![]() is open, closed, neither, or both.
is open, closed, neither, or both.
Solution
Consider the natural number 5. No matter what we choose ![]() to be, the
to be, the ![]() -neighborhood of 5 will contain some elements that are not natural numbers. Thus, there does not exist an epsilon neighborhood of 5 that is a subset of the natural numbers, and
-neighborhood of 5 will contain some elements that are not natural numbers. Thus, there does not exist an epsilon neighborhood of 5 that is a subset of the natural numbers, and ![]() is not open. For any natural number
is not open. For any natural number ![]() , let
, let ![]() . Since
. Since ![]() is the only natural number in the interval
is the only natural number in the interval ![]() , there exists an epsilon neighborhood for every natural number
, there exists an epsilon neighborhood for every natural number ![]() that does not intersect the set of natural numbers at any point other than
that does not intersect the set of natural numbers at any point other than ![]() . Thus, every natural number is not a limit point of
. Thus, every natural number is not a limit point of ![]() . For
. For ![]() , we can choose
, we can choose ![]() , where
, where ![]() is the distance from
is the distance from ![]() to the nearest natural number. So, for every
to the nearest natural number. So, for every ![]() , there exists an epsilon neighborhood that does not contain any natural numbers and consequently, does not intersect the set of natural numbers. Thus, any
, there exists an epsilon neighborhood that does not contain any natural numbers and consequently, does not intersect the set of natural numbers. Thus, any ![]() is not a limit point. Since there are not any limit points of
is not a limit point. Since there are not any limit points of ![]() that are not in
that are not in ![]() ,
, ![]() is closed.
is closed.
Example 41
Determine whether ![]() is open, closed, neither, or both.
is open, closed, neither, or both.
Solution
It is clear that for every real number ![]() there exists an epsilon neighborhood of
there exists an epsilon neighborhood of ![]() that is a subset of
that is a subset of ![]() . Thus,
. Thus, ![]() is open. No matter what we choose
is open. No matter what we choose ![]() to be, the
to be, the ![]() -neighborhood of every real number
-neighborhood of every real number ![]() contains other real numbers. So, every real number is a limit point of
contains other real numbers. So, every real number is a limit point of ![]() . Additionally, there are no limit points of
. Additionally, there are no limit points of ![]() not in
not in ![]() . Thus,
. Thus, ![]() is closed. Therefore,
is closed. Therefore, ![]() is both open and closed.
is both open and closed.
So, we have seen that sets can be open, closed, both, or neither. Now, we are going to look at another characteristic that only certain closed sets possess, compactness, along with a theorem that helps us prove a set is compact.
Heine-Borel Theorem
Before we can introduce the Heine-Borel Theorem, we need to define a couple more ideas related to sets, compactness and bounds. Both of the following definitions come from Abbott [1].
A set
A set
While it is possible to prove a set is compact by showing that every sequence in the set has a subsequence that converges to a limit that is also in the set, we have another method we can use to prove a sequence is compact, the Heine-Borel Theorem, which is stated by Abbott as follows [1].
Theorem IV.11 (Heine-Borel Theorem)
The proof of this theorem has two parts. The first is to show that if ![]() is compact, then it is closed and bounded. I will not copy it here as it is long and can be found in Abbott [1]. The second part is to show that if
is compact, then it is closed and bounded. I will not copy it here as it is long and can be found in Abbott [1]. The second part is to show that if ![]() is closed and bounded, then it is compact. I wrote this part of the proof as a homework problem for Introduction to Analysis. Within the proof, I will use the following theorem from Abbott [1].
is closed and bounded, then it is compact. I wrote this part of the proof as a homework problem for Introduction to Analysis. Within the proof, I will use the following theorem from Abbott [1].
Theorem IV.12
Let’s now prove that if ![]() is closed and bounded then it is compact.
is closed and bounded then it is compact.
Proof.
Because ![]() is bounded, every sequence
is bounded, every sequence ![]() is going to be bounded as well. By Theorem IV.19 in chapter 20, every
is going to be bounded as well. By Theorem IV.19 in chapter 20, every ![]() contains a convergent subsequence
contains a convergent subsequence ![]() . So, every sequence in
. So, every sequence in ![]() has a subsequence that converges to a limit. Now, we must show that for
has a subsequence that converges to a limit. Now, we must show that for ![]() ,
, ![]() .
.
Because ![]() and
and ![]() ,
, ![]() is a limit point of
is a limit point of ![]() by Theorem IV.12. (We can assume that
by Theorem IV.12. (We can assume that ![]() for all
for all ![]() because if the two were equal, then
because if the two were equal, then ![]() because
because ![]() , which is what we are trying to show.) So,
, which is what we are trying to show.) So, ![]() is a limit point of
is a limit point of ![]() . Because
. Because ![]() is closed, it contains its limit points. Thus,
is closed, it contains its limit points. Thus, ![]() . Therefore,
. Therefore, ![]() is compact.
is compact.
Let’s now work through an example that makes use of the Heine-Borel Theorem. This is a homework problem I completed for Introduction to Analysis that comes from Abbott [1]. This problem also makes use of another theorem from Abbott that I will state here so that what is done in the example makes sense [1].
Theorem IV.13
Example 42
Show that if ![]() is compact and
is compact and ![]() is closed, then
is closed, then ![]() is compact.
is compact.
Proof.
Because ![]() is compact,
is compact, ![]() is closed by Theorem IV.11. Because
is closed by Theorem IV.11. Because ![]() is also closed,
is also closed, ![]() is closed by Theorem IV.13. Because
is closed by Theorem IV.13. Because ![]() only contains elements that are in both
only contains elements that are in both ![]() and
and ![]() ,
, ![]() . Because
. Because ![]() is compact, it is bounded by Theorem IV.11. That is, there exists
is compact, it is bounded by Theorem IV.11. That is, there exists ![]() such that
such that ![]() for all
for all ![]() . Since every element
. Since every element ![]() is also in
is also in ![]() , it follows that
, it follows that ![]() for all
for all ![]() . Thus,
. Thus, ![]() is closed and bounded. Therefore,
is closed and bounded. Therefore, ![]() is compact by Theorem IV.13.
is compact by Theorem IV.13.
This concludes our discussion of the Topology of ![]() . We covered a lot of information, from the Axiom of Completeness and the density of
. We covered a lot of information, from the Axiom of Completeness and the density of ![]() and
and ![]() in
in ![]() to open and closed sets to compactness and the Heine-Borel Theorem. We even brought in some ideas connected to sequences, which we will discuss in more detail in the following section.
to open and closed sets to compactness and the Heine-Borel Theorem. We even brought in some ideas connected to sequences, which we will discuss in more detail in the following section.
