24 Rings
The formal definition of a ring is provided by Macauley as follows [17].
A ring
![]()
and
![]()
![]()
A ring ![]() is an additive abelian group. This means that the binary operation of addition must be commutative as well as satisfy all of the group axioms (closure, associativity, contains identity and inverses). Additionally,
is an additive abelian group. This means that the binary operation of addition must be commutative as well as satisfy all of the group axioms (closure, associativity, contains identity and inverses). Additionally, ![]() is defined under multiplication, which must satisfy the distributive property regardless of whether the element to be distributed is on the left or the right of the values to be distributed to. However, multiplication does not have to satisfy the group axioms. Some examples of rings include
is defined under multiplication, which must satisfy the distributive property regardless of whether the element to be distributed is on the left or the right of the values to be distributed to. However, multiplication does not have to satisfy the group axioms. Some examples of rings include ![]() and
and ![]() [17].
[17].
Our next section is on a specific type of ring known as an integral domain.
Integral Domains
Macauley provides us with the following definition for integral domains [17].
An integral domain is a commutative ring with 1 and with no nonzero zero divisors.
This definition brings in a few terms that we have not yet discussed. A commutative ring is one in which multiplication is commutative [7]. A ring with 1 contains a multiplicative identity that is not equal to the additive identity [7]. An element ![]() of a ring is a zero divisor if
of a ring is a zero divisor if ![]() or
or ![]() where
where ![]() [17]. So, an integral domain does not contain two nonzero elements whose product is zero.
[17]. So, an integral domain does not contain two nonzero elements whose product is zero.
We are now going to move on to fields, but we are not done with integral domains quite yet. We will provide a definition for fields and then work through a couple of proofs that show the relationship between fields and integral domains.
Fields
We already briefly discussed fields in Part IV: Chapter 18. Here, we are going to view fields from a different angle by looking at another definition and seeing how they connect to integral domains. The two definitions may look different, but keep in mind that they are defining the exact same idea, only with different words.
The definition of a field is given by Macauley as follows [17].
A set ![]() with addition and multiplication operations is a field if the following three conditions hold:
with addition and multiplication operations is a field if the following three conditions hold:
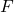 is an abelian group under addition.
is an abelian group under addition.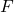 without
without  is an abelian group under multiplication.
is an abelian group under multiplication.- The distributive law holds:
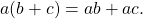
A field ![]() is an abelian group under addition. That is, the binary operation of addition is commutative and satisfies the group axioms. Furthermore,
is an abelian group under addition. That is, the binary operation of addition is commutative and satisfies the group axioms. Furthermore, ![]() without zero is an abelian group under multiplication. So, multiplication is commutative and satisfies the group axioms when 0 is excluded. The reason why we remove zero is that there does not exist a multiplicative inverse of zero in the real numbers [17]. So, if zero were included,
without zero is an abelian group under multiplication. So, multiplication is commutative and satisfies the group axioms when 0 is excluded. The reason why we remove zero is that there does not exist a multiplicative inverse of zero in the real numbers [17]. So, if zero were included, ![]() could not be a group under multiplication. Finally, the distributive law of multiplication holds.
could not be a group under multiplication. Finally, the distributive law of multiplication holds.
If we look closely, we can see that a field is a specific type of ring. A field is an abelian group under addition and is defined under multiplication that satisfies the associative property (because it is a group under multiplication) and the distributive law. Furthermore, a field is a commutative ring because it is an abelian group under multiplication. Finally, every element of the field other than zero has a multiplicative inverse in the field because it is a group under multiplication when zero is removed. We call these nonzero elements with multiplicative inverses units. So, a field is a commutative ring such that every nonzero element is a unit.
We will now look at a couple of proofs that show the relationship between fields and integral domains. Both proofs are ones that I have written for this paper. Additionally, the outline of the second proof comes from Macauley, but I wrote in the details [17].
Show that every field is an integral domain.
Proof.
Because an integral domain is a commutative ring, we need to show that every field is an abelian group under addition and is defined under multiplication that is commutative and satisfies the distributive law.By the first condition of definition V.13, every field is an abelian group under addition. By the second condition of the definition, every field is defined under multiplication that is commutative because a field without zero is an abelian group under multiplication. By the third condition of the definition, every field satisfies the distributive law
![]()
An integral domain is a commutative ring with 1 so we need to show that every field has an additive identity that is not equal to the multiplicative identity.
By the first and second conditions of definition V.13, every field is a group under addition and multiplication. So, every field contains the additive identity 0 and multiplicative identity ![]() .
.
Finally, an integral domain has no nonzero zero divisors. So, we need to show for any two elements ![]() and
and ![]() in a field that if
in a field that if ![]() is zero, then
is zero, then ![]() or
or ![]() is zero.
is zero.
Let ![]() and
and ![]() be elements of a field
be elements of a field ![]() . Because a field is a group under multiplication,
. Because a field is a group under multiplication, ![]() has a multiplicative inverse
has a multiplicative inverse ![]() in
in ![]() . So, if
. So, if ![]() , we have
, we have
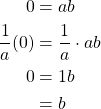
So, if ![]() where
where ![]() is not zero, it follows that
is not zero, it follows that ![]() must equal 0. Thus, a field does not contain any nonzero zero divisors. Therefore, every field is an integral domain.
must equal 0. Thus, a field does not contain any nonzero zero divisors. Therefore, every field is an integral domain.
Clearly, it is not the case that every integral domain is also a field because then calling a set an integral domain would be equivalent to calling it a field, which is not true. However, it is the case that every finite integral domain is a field. This brings us to our second proof.
Show that every finite integral domain is a field.
Proof.
By the first condition of definition V.13, every finite integral domain must be an abelian group under addition. By definition, an integral domain is a ring which is by a definition an abelian group under addition.By the second condition of definition V.13, every finite integral domain must be an abelian group under multiplication when 0 is excluded.
Because an integral domain is a group under addition, it follows that multiplication is closed and associative since multiplication is repeated addition. Because every integral domain is a ring with 1, every integral domain contains the multiplicative identity 1 that is not equal to the additive identity 0. All that remains is to show that a finite integral domain under multiplication contains inverses and that multiplication is commutative.
Let ![]() be an element of the finite integral domain
be an element of the finite integral domain ![]() . Because
. Because ![]() is finite, the sequence
is finite, the sequence
![]()
will eventually repeat itself. This implies that there exists ![]() , where
, where ![]() . So, we have,
. So, we have,
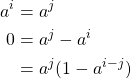
This implies that either ![]() or
or ![]() since
since ![]() does not have any nonzero zero divisors by definition. Furthermore, if
does not have any nonzero zero divisors by definition. Furthermore, if ![]() , we would have
, we would have
![]()
which implies that ![]() since
since ![]() does not contain any nonzero zero divisors. However, this contradicts
does not contain any nonzero zero divisors. However, this contradicts ![]() so
so ![]() . Thus,
. Thus,
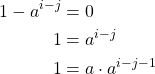
Therefore, every element in ![]() not equal to 0 has a multiplicative inverse that is also in
not equal to 0 has a multiplicative inverse that is also in ![]() .
.
Because every integral domain is a commutative ring, multiplication is commutative. Therefore, every finite integral domain is an abelian group under multiplication when 0 is excluded.
Finally, by the third condition of definition V.13, every field satisfies the distributive law. Because every integral domain is a ring by definition and every ring satisfies the distributive law by definition, every integral domain satisfies the distributive law.
Therefore, every finite integral domain is a field.
The following diagram provides a summary of how rings, integral domains, and fields are connected.
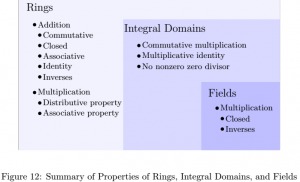
We are now going to look at rings of polynomials. Specifically, we are going to look at how to factor polynomials and how to prove that a polynomial cannot be factored.
