21 Limits and Continuity
We already mentioned limits and continuity of functions in Part I: Chapter 1. Instead of reiterating what was already discussed, we will introduce some new ideas, going deeper into limits and continuity. When we discussed limits before, we never actually gave a formal definition. So, we will start by defining limits using the following definition given by Abbott [1].
Let
Let’s now go through an example of how to use this definition. This example is a homework problem that I completed for Introduction to Analysis [6].
Show that
Proof.
Let ![]() .
.
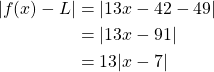
Let ![]() . So,
. So, ![]() implies
implies
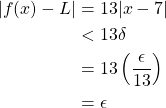
Therefore, ![]() .
.
When finding limits, we can combine our approaches from Calculus and Analysis. Calculus allows us to find a good candidate for the limit by doing what we did in Part I: Chapter 1. Analysis then allows us to prove that this candidate is in fact the limit by using definition IV.20 as just shown above. Now, we will explore continuity from an analysis perspective, looking at the Intermediate Value Theorem and uniform continuity.
Intermediate Value Theorem
We will start by presenting this theorem as it is given by Abbott [1].
Theorem IV.21 (Intermediate Value Theorem)
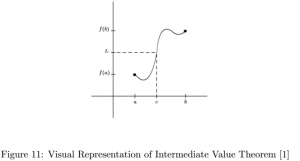
Let’s consider the image from Abbott above as we discuss what this theorem is saying. We have a continuous function ![]() whose domain is the closed interval
whose domain is the closed interval ![]() . So the graph of this function will have two endpoints,
. So the graph of this function will have two endpoints, ![]() and
and ![]() . There is also a real number
. There is also a real number ![]() between
between ![]() and
and ![]() . Now picture a horizontal line at
. Now picture a horizontal line at ![]() . Regardless of what continuous function we draw to connect the two endpoints, it will intersect the horizontal line at some point, and we can label this point as
. Regardless of what continuous function we draw to connect the two endpoints, it will intersect the horizontal line at some point, and we can label this point as ![]() . Therefore, there exists a point
. Therefore, there exists a point ![]() in the interval
in the interval ![]() where
where ![]() .
.
Let’s now look at an example of how this theorem can be used. The following problem is from Abbott and is a proof I completed as homework for Introduction to Analysis [1].
Show that it is impossible to have a continuous function defined on all of
Proof.
Consider a continuous function ![]() defined on all of
defined on all of ![]() with a range equal to
with a range equal to ![]() . That is,
. That is, ![]() is continuous. Because
is continuous. Because ![]() is continuous on every point in
is continuous on every point in ![]() ,
, ![]() is continuous on every point in a closed interval
is continuous on every point in a closed interval ![]() So,
So, ![]() is continuous. By Corollary IV.4.1 in chapter 19, there exists
is continuous. By Corollary IV.4.1 in chapter 19, there exists ![]() where
where
![]()
or
![]()
By the Intermediate Value Theorem, there exists ![]() such that
such that
![]()
This contradicts the range being equal to ![]() since
since ![]() . Thus,
. Thus, ![]() is not continuous which implies
is not continuous which implies ![]() is not continuous. Therefore, it is impossible to have a continuous function defined on all of
is not continuous. Therefore, it is impossible to have a continuous function defined on all of ![]() with range equal to
with range equal to ![]() .
.
So, this is the Intermediate Value Theorem (IVT). It is an example of an idea that seems so clear and obvious that mathematicians used it for years without a formal proof of its being true [1]. There does exist a proof for it now, but we will not cover it here. Instead, let’s move on to uniform continuity.
Uniform Continuity
We already introduced a definition for continuity of a function in Part I: Chapter 1, but now we will look at another definition for continuity of a function provided by Abbott [1].
A function
From the Calculus perspective, we said that a function ![]() was continuous at
was continuous at ![]() if
if
![]()
given that the limit exists and ![]() is defined. So, if
is defined. So, if ![]() is continuous at
is continuous at ![]() and the limit equals
and the limit equals ![]() , then
, then
![]()
Then, we can substitute ![]() for
for ![]() in definition IV.20, and we get the definition of continuity given above with a couple of differences.
in definition IV.20, and we get the definition of continuity given above with a couple of differences.
First, we do not state that ![]() is a limit point in the continuity definition. This is because the limit at
is a limit point in the continuity definition. This is because the limit at ![]() would not exist if
would not exist if ![]() were not a limit point. Since we are substituting
were not a limit point. Since we are substituting ![]() in for
in for ![]() , it is given that the limit exists so it would be redundant to restate that
, it is given that the limit exists so it would be redundant to restate that ![]() must be a limit point.
must be a limit point.
Second, in the limit definition, it is stated that
![]()
whereas the continuity definition says that
![]()
The difference is that the limit definition defines ![]() as not equal to
as not equal to ![]() . The reason is that the limit can still exist at
. The reason is that the limit can still exist at ![]() even if the function is not defined at
even if the function is not defined at ![]() . So, if we let
. So, if we let ![]() equal
equal ![]() and
and ![]() happens to be undefined,
happens to be undefined,
![]()
would not make sense. However, if a function is continuous at ![]() , it follows that
, it follows that ![]() is defined. So, we do not have to restrict
is defined. So, we do not have to restrict ![]() to not being equal to
to not being equal to ![]() .
.
Thus, using definition IV.20 along with the definition of continuity from Calculus, we arrive at the definition of continuity given above.
Uniform continuity is similar but a bit stricter than continuity. The definition of uniform continuity is given by Abbott as follows [1].
A function
The definitions of continuity and uniform continuity look very similar which makes it difficult to understand the difference between the two. As mentioned before, uniform continuity is a stricter form of continuity so a function can be continuous without being uniformly continuous. But if a function is uniformly continuous, it follows that the function is continuous.
A function is continuous if it is continuous at every point ![]() in its domain. So for a fixed
in its domain. So for a fixed ![]() ,
, ![]() can take on different values depending on
can take on different values depending on ![]() , and the function will still be continuous. The difference is that for a function to be uniformly continuous there must exist a single
, and the function will still be continuous. The difference is that for a function to be uniformly continuous there must exist a single ![]() for a fixed
for a fixed ![]() for all
for all ![]() in the domain [1].
in the domain [1].
We also have a theorem that helps with showing that a function is not uniformly continuous. What we use to disprove uniform continuity is the Sequential Criterion for Absence of Uniform Continuity. Abbott states it as follows [1].
Theorem IV.24 (Sequential Criterion for Absence of Uniform Continuity)
![]()
but
![]()
If we can find two sequences, ![]() and
and ![]() , in the domain of a function
, in the domain of a function ![]() such that the sequence
such that the sequence ![]() converges to 0 and the sequence
converges to 0 and the sequence ![]() is bounded below by a positive number, then
is bounded below by a positive number, then ![]() is not uniformly continuous.
is not uniformly continuous.
Let’s now look at an example that demonstrates how to prove a function is not uniformly continuous. This is a homework problem I completed for Introduction to Analysis that comes from Abbott [1].
Show that the continuous function
Proof.
Let ![]() with domain
with domain ![]() . Let
. Let ![]() ,
, ![]() and
and ![]()
If
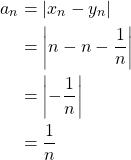
then ![]() Additionally,
Additionally,
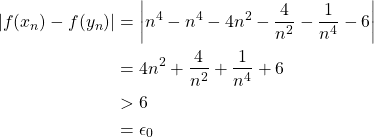
![]() . By Theorem IV.24,
. By Theorem IV.24, ![]() is not uniformly continuous on
is not uniformly continuous on ![]() .
.
Next, we will look at an example of how to show that a function is uniformly continuous. This example is a homework problem I completed for Introduction to Analysis that comes from Abbott [1].
Show that
Proof.
Consider the bounded subset of ![]()
![]() , where
, where ![]() .
.
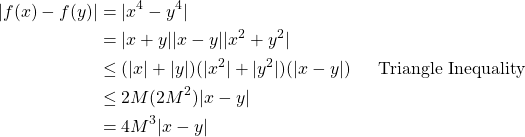
Let ![]() and
and ![]() . If
. If ![]() , then
, then
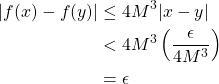
for all ![]() . Therefore,
. Therefore, ![]() is uniformly continuous on any bounded subset of
is uniformly continuous on any bounded subset of ![]() .
.
