30 Vector Spaces
Vector spaces are sets of vectors that must satisfy ten axioms. Consider the following definition from Larson and Valvo [16].
Let
-
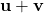 is in
is in 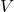 .
. -
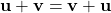
-
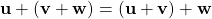
-
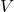 has a zero vector 0 such that for every u in
has a zero vector 0 such that for every u in 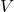 ,
, 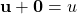 .
. - For every u in
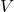 , there is a vector in
, there is a vector in 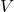 denoted by -u such that
denoted by -u such that 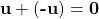 .
. -
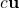 is in
is in 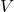 .
. -
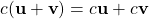 .
. -
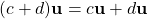 .
. -
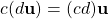 .
. - 1(u)=u.
The first column gives the axioms for addition. The vector space must be closed under addition, contain the additive identity (denoted by 0), and additive inverses. Furthermore, addition must be commutative and associative. The second column gives the rules for scalar multiplication. The vector space must be closed under scalar multiplication, and any vector multiplied by one must equal the vector itself. Furthermore, the associative property and distributive properties (distributing a scalar and distributing a vector) should hold.
Vectors come in a variety of forms. We already discussed vectors that can occur in ![]() -dimensional space. But vectors can also be functions, polynomials, and matrices [16]. Thus, certain sets of functions, polynomials, or matrices can be vector spaces.
-dimensional space. But vectors can also be functions, polynomials, and matrices [16]. Thus, certain sets of functions, polynomials, or matrices can be vector spaces.
Let’s work through the process of showing that a set of vectors is a vector space. This problem is one I completed for Elementary Linear Algebra and comes from Larson and Falvo [16].
Show that the set
Proof.
Consider the vectors ![]() ,
, ![]() , and
, and ![]() in
in ![]() .
.
Vector addition is closed because
![]()
which is an element of ![]() since
since ![]() is a real number. Vector addition is also commutative because
is a real number. Vector addition is also commutative because
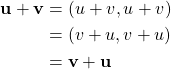
and associative because
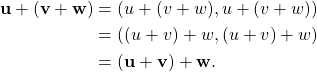
The zero vector ![]() is in
is in ![]() because 0 is a real number, and for every vector
because 0 is a real number, and for every vector ![]() in
in ![]() ,
,
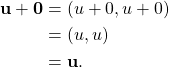
For every vector ![]() in
in ![]() , there exists
, there exists ![]() , which is in
, which is in ![]() because
because ![]() is a real number, such that
is a real number, such that
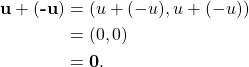
Scalar multiplication is closed because for every scalar ![]() ,
,
![]()
which is in ![]() because
because ![]() is a real number. Both distributive properties hold because
is a real number. Both distributive properties hold because
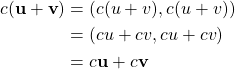
and
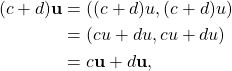
where ![]() and
and ![]() are scalars and u and v are vectors in
are scalars and u and v are vectors in ![]() .
.
Scalar multiplication is also associative because
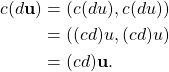
Finally,
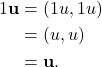
Because all ten axioms are satisfied, ![]() is a vector space.
is a vector space.
Vector spaces also have subspaces, which are defined by Larson and Falvo as follows [16].
A nonempty subset
In a vector space ![]() , there are always the two operations of vector addition and scalar multiplication. However, how these operations are defined may differ from one vector space to another [16].
, there are always the two operations of vector addition and scalar multiplication. However, how these operations are defined may differ from one vector space to another [16].
If we have a vector space ![]() and take a subset of those vectors, that subset is a subspace if it satisfies all of the axioms of a vector space for vector addition and scalar multiplication, which are defined the same way as they are in
and take a subset of those vectors, that subset is a subspace if it satisfies all of the axioms of a vector space for vector addition and scalar multiplication, which are defined the same way as they are in ![]() .
.
A special type of subspace of a vector space ![]() is known as the span of a subset
is known as the span of a subset ![]() of
of ![]() .
.
Spanning Sets
Larson and Falvo provide us with the following definitions [16].
A vector v in a vector space
![]()
where ![]() are scalars.
are scalars.
If
![]()
Let ![]() be a subset of a vector space
be a subset of a vector space ![]() . That is, every vector in
. That is, every vector in ![]() is also in
is also in ![]() . The span of
. The span of ![]() , denoted span(
, denoted span(![]() ), is the set of all vectors that can be “built” by adding together scalar multiples of the vectors in
), is the set of all vectors that can be “built” by adding together scalar multiples of the vectors in ![]() . Furthermore, span(
. Furthermore, span(![]() ) is a subspace of
) is a subspace of ![]() [16].
[16].
Sometimes, span(![]() ) is equal to
) is equal to ![]() . When this occurs, we say that
. When this occurs, we say that ![]() is a spanning set of
is a spanning set of ![]() and that
and that ![]() spans
spans ![]() [16]. Let’s look at an example of how to show that a subset
[16]. Let’s look at an example of how to show that a subset ![]() of a vector space
of a vector space ![]() spans
spans ![]() . This is a problem I completed for Elementary Linear Algebra and comes from Larson and Falvo [16].
. This is a problem I completed for Elementary Linear Algebra and comes from Larson and Falvo [16].
Show that the set
Proof.
To prove this, we need to show that there exist scalars ![]() ,
, ![]() , and
, and ![]() such that for every vector
such that for every vector ![]() in
in ![]() ,
,
![]()
By scalar multiplication and vector addition, we have
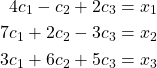
This is a system of equations which has a unique solution if and only if the determinant of the coefficient matrix (matrix consisting of only the coefficients) is not equal to zero [16]. So, we need to find the determinant of
![Rendered by QuickLaTeX.com \[\left[ \begin{array}{@{}*{7}{r}@{}} 4 & -1&2\\ 7&2&-3 \\ 3&6&5 \end{array} \right].\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fd9ab6f06f953c9dc1ae3c8eb9807e6c_l3.png)
By Theorem VI.3 in chapter 28, the determinant is equal to the sum of the products of each entry with its cofactor (see definition VI.2 in chapter 28) for every entry in whichever row or column we choose. Let’s go with the first column.
We need to find cofactors ![]() ,
, ![]() , and
, and ![]() by first finding the minors
by first finding the minors ![]() ,
, ![]() and
and ![]() . Deleting the first row and first column of the coefficient matrix gives us
. Deleting the first row and first column of the coefficient matrix gives us
![]()
with determinant
![]()
which means
![]()
Deleting the second row and first column of the coefficient matrix gives us
![]()
with determinant
![]()
which means
![]()
Deleting the third row and first column of the coefficient matrix gives us
![]()
with determinant
![]()
which means
![]()
So, the determinant of ![Rendered by QuickLaTeX.com \left[ \begin{array}{@{}*{7}{r}@{}} 4 & -1&2\\ 7 & 2&-3 \\ 3 & 6&5 \\ \end{array} \right]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f3667b15fc9af1a00c0de25a9b388062_l3.png) is
is
![]()
This means that our system of equations has a unique solution for all real numbers ![]() ,
, ![]() , and
, and ![]() . This is because the determinant of the coefficient matrix is not equal to zero if and only if the system of equations has a unique solution [16]. Thus, for every vector
. This is because the determinant of the coefficient matrix is not equal to zero if and only if the system of equations has a unique solution [16]. Thus, for every vector ![]() in
in ![]() , we can find
, we can find ![]() ,
, ![]() , and
, and ![]() such that
such that
![]()
Therefore, ![]() spans
spans ![]() .
.
We will now discuss a specific type of subset that spans a vector space, which is referred to as a basis for that vector space.
Basis
In essence, a basis ![]() of a vector space
of a vector space ![]() is the largest set of independent vectors such that every vector in
is the largest set of independent vectors such that every vector in ![]() can be written as a linear combination of vectors in
can be written as a linear combination of vectors in ![]() . Consider the following definition from Larson and Falvo [16].
. Consider the following definition from Larson and Falvo [16].
A set of vectors
-
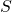 spans
spans 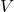 .
. -
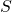 is linearly independent.
is linearly independent.
The condition that ![]() spans
spans ![]() ensures that every vector in
ensures that every vector in ![]() can be formed by some linear combination of vectors in
can be formed by some linear combination of vectors in ![]() . However, it is possible to have more vectors in a spanning set than are actually needed. This can happen if one of the vectors in a spanning set can itself be written as a linear combination of the other vectors in the spanning set. Thus, the condition that
. However, it is possible to have more vectors in a spanning set than are actually needed. This can happen if one of the vectors in a spanning set can itself be written as a linear combination of the other vectors in the spanning set. Thus, the condition that ![]() is linearly independent ensures that we have the minimum number of vectors needed in order to span
is linearly independent ensures that we have the minimum number of vectors needed in order to span ![]() because a set of vectors is linearly independent if none of the vectors can be written as a linear combination of the other vectors [16]. The formal definition is given by Larson and Falvo as follows [16].
because a set of vectors is linearly independent if none of the vectors can be written as a linear combination of the other vectors [16]. The formal definition is given by Larson and Falvo as follows [16].
A set of vectors
![]()
has only the trivial solution ![]() If there are also nontrivial solutions, then
If there are also nontrivial solutions, then ![]() is called linearly dependent.
is called linearly dependent.
Let’s now look at a problem that I completed for Elementary Linear Algebra that comes from Larson and Falvo [16].
Is the set of vectors
![]()
a basis for ![]() ?
?
Solution
By example 63, we know that ![]() spans
spans ![]() . So, all we have to do is see whether the vectors in
. So, all we have to do is see whether the vectors in ![]() are linearly independent. By definition VI.9, the set of vectors in
are linearly independent. By definition VI.9, the set of vectors in ![]() are linearly independent if and only if the equation
are linearly independent if and only if the equation
![]()
has only the trivial solution. From our equation, we have the following system
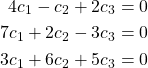
As we saw in Example 63, this system of equations has a unique solution because the determinant of the coefficient matrix is not zero. Because the solution is unique and ![]() , and
, and ![]() is a solution,
is a solution, ![]() , and
, and ![]() is the only solution. Thus, the set of vectors in
is the only solution. Thus, the set of vectors in ![]() are linearly independent by definition VI.9. Therefore,
are linearly independent by definition VI.9. Therefore, ![]() is a basis for
is a basis for ![]() by definition VI.8.
by definition VI.8.
In our next section, we will discuss row and column spaces of matrices.
