40 Game Theory: Total Conflict Game

The final topic of modeling that we will be discussing is game theory. Game theory models the decisions of two or more individuals or groups of individuals given a situation [8]. Using game theory, we can model how different species interact within a habitat [8]. Will they coexist, or will one dominant the others? We can also model how corporations may compete [8]. Will they reach a compromise, or will one bankrupt the others? Those are just a couple of many different scenarios that can be modeled with game theory.

Because there is so much that we could talk about relating to game theory and it would be impossible for us to cover it all, we are going to focus on the total conflict game along with a few strategies that can be used in a total conflict game.

A total conflict game between two players is one in which one player’s payoff increases if and only if the other player’s payoff decreases [8]. Consider the following situation based off of one from Giordano et al. [8],

Rose’s choices are and . Colin’s are and . The first value in each ordered pair represents Rose’s payoff, and the second, Colin’s payoff. Notice that whenever Rose’s payoff increases Colin’s payoff decreases.

Using this game, we can study how outcomes change as different rules are put in place. Our first scenario is playing without communication.

Playing Without Communication

One way a total conflict game may be played is if no player communicates with another. That is, each player must make his decision based off of what he thinks the other players will decide. The strategy used to accomplish this is the maxmin strategy [8]. Basically, each player chooses the maximum of his minimum payoffs. That is, when Rose utilizes this strategy, she looks at the worst payoff she will get for and for , then chooses whichever row has the maximum minimum payoff. This strategy works the same way from Colin’s perspective. Let’s look at our game again.

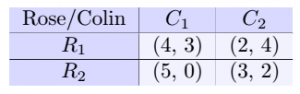
Using the maxmin strategy, Rose sees that in her minimum payoff is 2 and in is 3. So, she is going to go with since 3 is larger than 2. Similarly, Colin sees that his minimum payoff in is 0 and in is 2. So, Colin will choose because 2 is larger than 0. Because and intersect at (3, 2), Rose will receive a payoff of 3, and Colin a payoff of 2.

Now, let’s examine what happens when the players can communicate.

Playing With Communication

Another way the total conflict game can be played is that the players do communicate with one another. That is, the second player knows what choice the first player has made when he makes his decision. Let’s look at our game again and consider two cases, Rose goes first and Colin goes first.

We will first consider what happens when Rose goes first. Rose knows that if she chooses , then Colin will choose to maximize his payoffs. Thus, her payoff would be 2. But if she chooses , Colin will choose , and she will get a payoff of 3. Therefore, Rose decides to choose , giving her a payoff of 3 and Colin a payoff of 2.

Now, we will let Colin go first and see what happens. Colin knows if he chooses then Rose will choose to maximize her payoff, giving him a payoff of 0. However, if he chooses , Rose will choose , giving him a payoff of 2. Therefore, Colin chooses , giving him a payoff of 2 and Rose a payoff of 3.

However, the game is not over because Rose still has a couple tricks up her sleeve. She is not content with her payoff of 3 and wants to get the payoff of 4 or 5. Since Colin is going first, she needs to either convince him to choose by a promise or make him choose by a threat.

The threat strategy is one where Rose threatens to hurt Colin if he chooses even if it hurts her as well [8]. For this particular game, the threat strategy will not do anything. She cannot threaten to choose if Colin chooses since Colin knows she will choose , threat or no threat. She cannot threaten Colin with choosing since her choosing actually benefits Colin.

But Rose has one more option, the promise strategy. This strategy is one where Rose promises to choose an option that hurts her and benefits Colin if he chooses [8]. In this particular game, Rose promises to choose if Colin chooses . If Colin chooses , this promise ensures that he will get a payoff of 3 instead of 0. Additionally, this promise ensures that Rose “hurts” herself since she is foregoing the payoff of 5 for a payoff of 4. Without the promise, Colin gets a payoff of 2 and Rose a payoff of 3. So, the promise strategy will actually work in favor of both of them because Colin will get a payoff of 3 and Rose a payoff of 4.