37 Linear and Cubic Splines
In the last section, we looked at how to fit a Lagrangian polynomial to a data set. However, a Lagrangian polynomial can quickly become a polynomial with a very high order, which is disadvantageous for a couple of reasons.
Let ![]() represent the independent variable and
represent the independent variable and ![]() the dependent variable. One disadvantage is that the polynomial oscillates a lot near the smallest value and largest value for
the dependent variable. One disadvantage is that the polynomial oscillates a lot near the smallest value and largest value for ![]() [8]. This leads to a lot of error in the prediction of the corresponding
[8]. This leads to a lot of error in the prediction of the corresponding ![]() when
when ![]() is equal to a number near the smallest or largest
is equal to a number near the smallest or largest ![]() values.
values.
Another disadvantage is that the coefficients of the polynomial are very sensitive to small changes in the data [8]. This means a slight difference in rounding or a small measuring error may result in a polynomial that is much different than the polynomial that would have been used otherwise. This too leads to inaccurate predictions.
Because of these disadvantages, we will look at two more modeling methods, linear splines and cubic splines, that allow us to model the given data and predict the corresponding ![]() for an
for an ![]() that is between the smallest and largest values given in the data for the independent variable.
that is between the smallest and largest values given in the data for the independent variable.
Linear Splines
Consider a data set of independent values ![]() in increasing order and corresponding dependent values
in increasing order and corresponding dependent values ![]() The method of linear splines is to find a line to connect each pair of adjacent points. That is, we find the equation of the line that connects
The method of linear splines is to find a line to connect each pair of adjacent points. That is, we find the equation of the line that connects ![]() and
and ![]() , the line that connects
, the line that connects ![]() and
and ![]() , and so on until we find the line that passes through
, and so on until we find the line that passes through ![]() and
and ![]() [8]. Each of these lines is referred to as a spline. Let’s look at an example of how to this. I completed this problem for Mathematical Models/Applications 2 [26].
[8]. Each of these lines is referred to as a spline. Let’s look at an example of how to this. I completed this problem for Mathematical Models/Applications 2 [26].
Find the linear splines for the following data set and predict the
![]()
Solution
A linear spline is of the form ![]() Since the first spline
Since the first spline ![]() must pass through (14, 320) and (22, 490), we have the following system of equations.
must pass through (14, 320) and (22, 490), we have the following system of equations.
![]()
Subtracting the top equation from the bottom one gives us
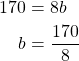
Substituting ![]() into the first equation gives us
into the first equation gives us
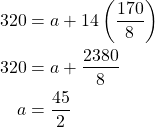
Therefore,
![]()
Following the same method, it can be found that
![Rendered by QuickLaTeX.com \begin{align*} S_2(x)&=\frac{705}{2}+\frac{25}{4}x &&\text{with domain $[22,30]$}\\ S_3(x)&=690-5x &&\text{with domain $[30,38]$}\\ S_4(x)&=595-\frac{5}{2}x &&\text{with domain $[38,46].$}\\ \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-527431a85a1043e72f051dc4a4ce640c_l3.png)
Because ![]() , we will use the third linear spline to predict the
, we will use the third linear spline to predict the ![]() -value for
-value for ![]() .
.
![]()
Linear splines are first-order polynomials and are quite accurate. However, we can also use third-order polynomials, called cubic splines, that are sometimes more accurate depending on the data.
Cubic Splines
The method of cubic splines is very similar to that of linear splines. We want to find a curve for each pair of adjacent points by finding the equation of a second-degree polynomial, or cubic spline, that connects each pair [8]. Let’s go through the following problem that I completed for Mathematical Models/Applications 2 [26].
Find the natural cubic splines for the following data set.
![]()
Solution
Because we have three sets of points, we need to find two cubic splines, ![]() and
and ![]() . Because we have eight different variables to solve for, we need a system of eight equations. Because the first spline connects (2, 2) and (4, 8), we have
. Because we have eight different variables to solve for, we need a system of eight equations. Because the first spline connects (2, 2) and (4, 8), we have
(1) ![]()
Similarly, because the second spline connects (4, 8) and (7, 12), we have
(2) ![]()
These next equations involve derivatives (see Part I: Chapter 2). We know that the slope at (4, 8) is the same for both splines. That is, ![]() . Because
. Because ![]() and
and ![]() , we have
, we have
![]()
which is equivalent to
(3) ![]()
Furthermore, because the first derivatives are equal, the second derivatives, ![]() and
and ![]() are equal as well. Because
are equal as well. Because ![]() and
and ![]() , we have
, we have
![]()
which is equivalent to
(4) ![]()
Finally, because we are asked to find the natural cubic spline, the second derivatives at the exterior points, ![]() and
and ![]() , are equal to zero [8]. This gives us
, are equal to zero [8]. This gives us
(5) ![]()
We can represent this system of eight equations as an equation of matrices the following way.
![Rendered by QuickLaTeX.com \[\left[ \begin{array}{@{}*{8}{r}@{}} 1&2&4&8&0&0&0&0\\ 1&4&16&64&0&0&0&0\\ 0&0&0&0&1&4&16&64\\ 0&0&0&0&1&7&49&343\\ 0&1&8&48&0&-1&-8&-48\\ 0&0&2&24&0&0&-2&-24\\ 0&0&2&12&0&0&0&0\\ 0&0&0&0&0&0&2&42\\ \end{array} \right]\left[ \begin{array}{@{}*{7}{r}@{}} a\\ b\\ c\\ d\\ e\\ f\\ g\\ h\\ \end{array} \right]=\left[\begin{array}{@{}*{7}{r}@{}} 2\\ 8\\ 8\\ 12\\ 0\\ 0\\ 0\\ 0\\ \end{array} \right]\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5e8023b8f9d71541fddb3589e31dece4_l3.png)
Using Excel, we can find the inverse of the first matrix which is
![Rendered by QuickLaTeX.com \[\left[ \begin{array}{@{}*{8}{r}@{}} 2&-1&0&0&0&0&4&0\\ -0.3&0.3&-0.13&0.13&0.4&0.4&-3.8&-0.2\\ -0.15&0.15&0.1&-0.1&-0.3&-0.3&1.1&0.15\\ 0.03&-0.03&-0.02&0.02&0.05&0.05&-0.1&-0.03\\ 4.67&-4.67&-0.78&1.78&9.33&-6.22&-3.11&-6.22\\ -2.3&2.3&1.2&-1.2&-4.6&3.07&1.53&4.47\\ 0.35&-0.35&-0.23&0.23&0.7&-0.47&-0.23&-1.02\\ -0.02&0.02&0.01&-0.01&-0.03&0.02&0.01&0.07\\ \end{array} \right]\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d8e8d5dac7ff2ecc5e0ca539cae4f031_l3.png)
Multiplying both sides of the equation by this matrix gives us
![]()
and
![]()
which gives us the following cubic splines:
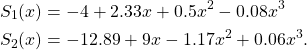
We have now seen a few different ways that we can model data. We can find one polynomial that passes through all of the data points, such as a Lagrangian polynomial, which works as long as we only have a few data points. If we have many data points, a more accurate model can be derived by using splines.
Our next topic is on how we can model probabilistic behavior and predict behavior long-term using Markov chains.
