11 Proof Techniques
As we mentioned before, proofs are critical in the realm of mathematics so it is important to know how to properly prove a statement by using the correct method. There are five techniques that we will be discussing.
- Direct Proofs: A direct proof is appropriate when we can reach the conclusion directly from the assumption through a series of logical steps. We start with the assumption itself then show through logical steps that the conclusion must be true. Proofs in a high-school geometry course usually follow this format.
- Contraposition: This method of proof proves the statement by proving the contrapositive of the statement. This is appropriate when it is easier to prove the contrapositive than it is to prove the original statement.
- Indirect Proofs: An indirect proof can also be referred to as a proof of contradiction. With this method, we assume that our statement
 is not true then show through a series of logical steps that we reach a contradiction. Because of the contradiction, our assumption has been shown to be false which proves that the original statement is in fact true. This method is appropriate when it is easier to show that
is not true then show through a series of logical steps that we reach a contradiction. Because of the contradiction, our assumption has been shown to be false which proves that the original statement is in fact true. This method is appropriate when it is easier to show that  is true through this contradiction method than it is to prove the statement directly.
is true through this contradiction method than it is to prove the statement directly. - Mathematical Induction: Mathematical induction is an interesting proof method that consists of two steps, the basis step and the inductive step. This method is useful when proving statements about the integers [22]. Proofs relating to sequences and series usually use this method.
- Proof by Cases: Proof by cases is a proof that is broken into smaller pieces that are then proved individually. This is appropriate when it is necessary (or perhaps easier) to prove individual parts rather than the whole at one time.
We will now explore each of these in depth in the following sections.
Direct Proofs
In a direct proof, we start with our assumption and work through a series of logical steps to reach what we are trying to prove, taking a straight path from start to finish. We do not have to go one of the roundabout ways such as proving the contrapositive or proving by contradiction. Whenever we need to prove a statement, we should first look at the direct proof method and see if it will work as this is the most straightforward of the proof techniques. There is no need to make the process more complicated than it needs to be.
Let’s look at an example to have a better idea of what a direct proof actually looks like. This proof is a homework problem I completed for Number Theory and comes from Rosen [22]. Keep in mind that an integer ![]() divides an integer
divides an integer ![]() , denoted as
, denoted as ![]() , if and only if there exists an integer
, if and only if there exists an integer ![]() such that
such that ![]() .
.
Show that if
Proof.
We are given that ![]() is a divisor of
is a divisor of ![]() . This means that there is an integer
. This means that there is an integer ![]() such that
such that
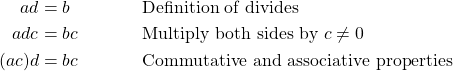
Thus, ![]() is a divisor of
is a divisor of ![]() . Therefore,
. Therefore, ![]() .
.
Notice how we started with what we were given and followed clear, logical steps to our conclusion.
Sometimes, a direct proof is not the best method. It may be easier to prove the contrapositive.
Contraposition
For the statement “if ![]() , then
, then ![]() ,” the contrapositive statement is “if not
,” the contrapositive statement is “if not ![]() , then not
, then not ![]() .”
.”
In essence, the proof method of contraposition consists of proving the contrapositive of the statement rather than the statement itself. The reason why this method works is that a statement and its contrapositive are equivalent. This is proven by contradiction in the following section.
The proof that we will look at to demonstrate the contrapositive method is one I completed for Introduction to Analysis which is a homework problem from Abbott [1]. To help clarify the logic, the theorem used in the proof is given by Abbott as follows [1].
Theorem II.2
Additionally, Definition IV.14 from chapter 20 is also used.
Show that if
Proof.
By Theorem II.2, ![]() converges to 0 since
converges to 0 since ![]() converges. By Definition IV.14, for
converges. By Definition IV.14, for ![]() 0,
0, ![]() such that when
such that when ![]() ,
,
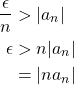
Thus, ![]() converges to 0 by Definition IV.14. Therefore, if
converges to 0 by Definition IV.14. Therefore, if ![]() for all
for all ![]() and
and ![]() converges to
converges to ![]() with
with ![]() , then the series
, then the series ![]() diverges, using proof by contraposition.
diverges, using proof by contraposition.
Indirect Proofs (Proofs by Contradiction)
An indirect proof, or proof by contradiction, works well when proving that an implication ![]() is true. The method is to assume that the implication is false. Recall from the truth table in chapter 10 that the only possible way for the implication
is true. The method is to assume that the implication is false. Recall from the truth table in chapter 10 that the only possible way for the implication ![]() to be false is if there is an instance where
to be false is if there is an instance where ![]() is true but
is true but ![]() is false. Thus, we begin the contradiction method by assuming that
is false. Thus, we begin the contradiction method by assuming that ![]() is true and
is true and ![]() is false. Then, we show (usually directly) that we reach
is false. Then, we show (usually directly) that we reach ![]() for some other statement
for some other statement ![]() when this assumption is true. Because it is a logical impossibility to have
when this assumption is true. Because it is a logical impossibility to have ![]() , we know that our assumption cannot possibly be true. Since our assumption is the only possible way that the original implication
, we know that our assumption cannot possibly be true. Since our assumption is the only possible way that the original implication ![]() could be false, we have shown that the implication must be true.
could be false, we have shown that the implication must be true.
The following homework problem from Abbott, which I completed for Introduction to Analysis, demonstrates this [1].
Show that if
Proof.
Suppose there exists ![]() and
and ![]() such that
such that ![]() where
where ![]() . This implies that
. This implies that ![]() since a real number must either be rational or irrational. Because
since a real number must either be rational or irrational. Because ![]() is closed under addition,
is closed under addition, ![]() . This contradicts
. This contradicts ![]() . By this contradiction,
. By this contradiction, ![]() if
if ![]() and
and ![]() .
.
In the last section, we mentioned that a statement and its contrapositive are logically equivalent. This next proof that I wrote will show us the reasoning behind the contrapositve method.
Show that
Proof.
Because this is an if and only if statement, we must prove it in two parts. The first part is to show that if ![]() then
then ![]() . The second part is to show that if
. The second part is to show that if ![]() then
then ![]() .To prove the first part, suppose that
.To prove the first part, suppose that ![]() true but
true but ![]() is false. The only way that the implication can be false is if
is false. The only way that the implication can be false is if ![]() is true and
is true and ![]() is not so we have
is not so we have ![]() . But,
. But, ![]() is true. So if we have
is true. So if we have ![]() , we must have
, we must have ![]() . Thus, if
. Thus, if ![]() is true but
is true but ![]() is false, we have
is false, we have ![]() , which is a logical impossibility. Thus, if
, which is a logical impossibility. Thus, if ![]() is true, then
is true, then ![]() must be true as well.
must be true as well.
To prove the second part, suppose that ![]() is true but
is true but ![]() is false. The only way that the implication can be false is if
is false. The only way that the implication can be false is if ![]() is true and
is true and ![]() is not so we have
is not so we have ![]() . But,
. But, ![]() is true. So if we have
is true. So if we have ![]() , we must have
, we must have ![]() . Thus, if
. Thus, if ![]() is true but
is true but ![]() is false, we have
is false, we have ![]() , which is a logical impossibility. Thus, if
, which is a logical impossibility. Thus, if ![]() is true, then
is true, then ![]() must be true as well.
must be true as well.
Therefore, ![]() if and only if
if and only if ![]() .
.
So, we have just proven that a statement and its contrapositive are equivalent. Thus, if the statement is true, the contrapositive is true and vice versa. This is why we can use the proof by contraposition method. Let’s now move on to one of the most interesting proof methods, mathematical induction.
Mathematical Induction
Mathematical induction is useful when proving statements about the natural or whole numbers, especially when related to sequences or series. For example, recall in Part I: Chapter 6, we discussed how to prove sequences converged using the Monotone Convergence Theorem. Induction is a great tool that allows us to prove that a sequence is monotone and bounded so that we may use the Monotone Convergence Theorem.
In general, induction follows a two-step process. We begin with the basis step in which we prove that the base case is true. Then, we have the inductive step that shows every other case is true by using the inductive hypothesis. Probably the best way to understand what all of this means is to look at an example. The following proof is a homework problem that I completed for Introduction to Analysis [6].
Prove that the sequence defined by
![]()
for ![]() converges.
converges.
Proof.
We will prove this by using induction to show that the sequence is bounded and monotone. Then by the Monotone Convergence Theorem, we will have proven that the sequence converges.So first, we will use induction to show that the sequence is bounded above. We begin with the basis step in which we show that the first term of the sequence is less than or equal to some real number ![]() .
.
The next step is the inductive step in which we show that every other number in the sequence is also less than or equal to ![]() . We do this by using the inductive hypothesis. The inductive hypothesis assumes that there is some number
. We do this by using the inductive hypothesis. The inductive hypothesis assumes that there is some number ![]() in the sequence that is less than or equal to
in the sequence that is less than or equal to ![]() . Then, we show that
. Then, we show that ![]() must also be less than or equal to
must also be less than or equal to ![]() .
.
- Basis Step:
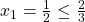 .
. - Inductive Step: The inductive hypothesis is “assume
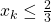 for some
for some 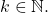 ” Show that
” Show that 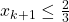 .
.
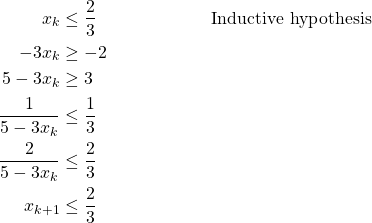
By mathematical induction, the sequence is bounded above by ![]() .
.
Now, we need to use induction to show that the sequence is nondecreasing. We begin with the basis step in which we show that the first term of the sequence is less than or equal to the second term in the sequence.
In this case, the inductive hypothesis is that there exists some number ![]() in the sequence that is less than or equal to
in the sequence that is less than or equal to ![]() . We then use this in the inductive step to show that if
. We then use this in the inductive step to show that if ![]() is less than or equal to
is less than or equal to ![]() then
then ![]() is less than or equal to
is less than or equal to ![]() .
.
- Basis Step:
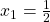 , and
, and 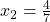 . Therefore,
. Therefore, 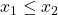 .
. - Inductive Step: The inductive hypothesis is “assume
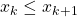 for some
for some 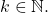 ” Show that
” Show that 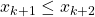 .
.

Therefore, the sequence is monotone by mathematical induction. Because the sequence is monotone, bounded below by ![]() , and bounded above by
, and bounded above by ![]() , the sequence converges by the Monotone Convergence Theorem.
, the sequence converges by the Monotone Convergence Theorem.
Let’s now try to understand why induction works. Consider the section of the proof where we showed the sequence is bounded above. With the induction step, we showed that if ![]() then it must be the case that
then it must be the case that ![]() as well. The basis step proved that
as well. The basis step proved that ![]() which implies
which implies ![]() which then implies
which then implies ![]() and so on. Thus, every term in the sequence must be less than or equal to
and so on. Thus, every term in the sequence must be less than or equal to ![]() . Similar reasoning can be used to explain why induction works when proving the sequence is monotone. In general, this is why induction proves a statement to be true when the basis step is established and the inductive step can be proven using the inductive hypothesis.
. Similar reasoning can be used to explain why induction works when proving the sequence is monotone. In general, this is why induction proves a statement to be true when the basis step is established and the inductive step can be proven using the inductive hypothesis.
Let’s now move on to our final proof method, proof by cases.
Proof by Cases
A proof by cases is simply a proof that we break into smaller parts, or cases. We use this method when it is easier or even mandatory to prove individual cases rather than everything at once. The best way to understand this method is to see an example. The following proof is a homework problem I completed for Number Theory and comes from Rosen [22]. To help clarify the logic, the theorem used in the proof is given by Rosen as follows [22].
Theorem II.3 (The Fundamental Theorem of Arithmetic)
Show that every positive integer can be written as the product of a square (possibly 1) and a square-free integer. A square-free integer is an integer that is not divisible by any perfect squares other than 1.
Proof.
![]() Because 1 is a square and a square-free integer, 1 can be written as the product of a square and a square-free integer.Let
Because 1 is a square and a square-free integer, 1 can be written as the product of a square and a square-free integer.Let ![]() be a positive integer.
be a positive integer.
![]()
where ![]() is prime,
is prime, ![]() , and
, and ![]() is a positive integer by the Fundamental Theorem of Arithmetic.
is a positive integer by the Fundamental Theorem of Arithmetic.
Case 1: ![]() is even for
is even for ![]() .
.
This means that
![]()
where ![]() and
and ![]() is a positive integer. So,
is a positive integer. So,
![]()
Let ![]() Therefore,
Therefore, ![]() , and
, and ![]() is the product of a square and a square-free integer.
is the product of a square and a square-free integer.
Case 2: ![]() is odd for
is odd for ![]() .
.
This means that
![]()
where ![]() and
and ![]() is an integer. So,
is an integer. So,
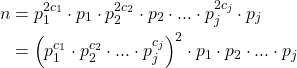
Let ![]() and
and ![]() Thus,
Thus, ![]()
Because ![]() ,
, ![]() is not divisible by any perfect squares other than 1. Therefore,
is not divisible by any perfect squares other than 1. Therefore, ![]() is the product of a square and a square-free integer.
is the product of a square and a square-free integer.
Case 3: The prime-power factorization of ![]() contains at least one prime raised to an even power and at least one prime raised to an odd power.
contains at least one prime raised to an even power and at least one prime raised to an odd power.
Rewrite the prime-power factorization of ![]() so that all primes to an even power are grouped together and all primes to an odd power are grouped together. That is,
so that all primes to an even power are grouped together and all primes to an odd power are grouped together. That is,
![]()
where ![]() and
and ![]() are prime,
are prime, ![]() and
and ![]() , and
, and ![]() and
and ![]() are integers. So,
are integers. So,
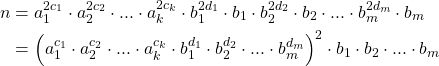
Let ![]() and
and ![]() . Thus,
. Thus, ![]() .
.
Because ![]() ,
, ![]() is not divisible by any perfect squares other than 1. Thus,
is not divisible by any perfect squares other than 1. Thus, ![]() is the product of a square and a square-free integer.
is the product of a square and a square-free integer.
Therefore, every positive integer can be written as the product of a square and a square-free integer.
Notice that in our proof, the cases covered every single possibility. The prime factorization of a positive integer greater than 1 consists of the product of primes raised to some power. The primes can all be raised to an even power, all raised to an odd power, or some can be raised to an even and some to an odd. These are our only possibilities, and we provided a short proof for each one, referred to as cases. It is critical when using this method that we address every single possibility.
