Row and Column Spaces

Abigail Huettig

31 Row and Column Spaces

For every matrix $A$ , $A$ has row vectors and column vectors. Each row of a matrix is a row vector of that matrix. Similarly, each column is a column vector of that matrix. Using these vectors, we can find a basis for the row space and column space of $A$ . Let’s look at the definition for row spaces and column spaces as given by Larson and Falvo [16].

Definition VI.10
Let $A$ be an $m\times n$ matrix.

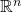The row space of $A$ is the subspace of $\mathbb{R}^n$ spanned by the row vectors of $A$ .
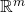The column space of $A$ is the subspace of $\mathbb{R}^m$ spanned by the column vectors of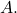 $A.$

Because the row vectors of a matrix $A$ span the row space of $A$ , we can find the basis of the row space by removing any row vectors that can be written as a linear combination of the other row vectors. Similarly, the column vectors of $A$ span the column space of $A$ . So, we can find the basis of the column space by removing any column vectors that can be written as a linear combination of the other column vectors.

Before demonstrating these ideas with an example, it is helpful to have the following theorem from Larson and Falvo to make our work easier [16].

Theorem VI.11 (Basis for the Row Space of a Matrix)

If a matrix $A$ is row-equivalent to a matrix $B$ in row-echelon form, then the nonzero row vectors of $B$ form a basis for the row space of $A$ .

Now, let’s work through an example that I completed for Elementary Linear Algebra that comes from Larson and Falvo [16].

Example 65
Find a basis for the row space and a basis for the column space of the matrix

$\left[ \begin{array}{@{}*{7}{r}@{}} 1&-3&2\\ 4&2&1 \\ \end{array} \right]$

Solution
To find a basis for the row space, we first need to convert our matrix into row-echelon form using elementary row operations.

$\begin{align*} &\left[ \begin{array}{@{}*{7}{r}@{}} 1&-3&2\\ 4&2&1 \\ \end{array} \right] &&\text{$-4R_1+R_2\rightarrow R_2$}\\ &\left[ \begin{array}{@{}*{7}{r}@{}} 1&-3&2\\ 0&14&-7 \\ \end{array} \right] &&\text{$\frac{1}{14}R_2\rightarrow R_2$}\\ &\left[ \begin{array}{@{}*{7}{r}@{}} 1&-3&2\\ 0&1&-\frac{1}{2} \\ \end{array} \right] &&\text{$3R_2+R_1\rightarrow R_1$} \\ &\renewcommand{\arraystretch}{1.5}\left[ \begin{array}{@{}*{7}{r}@{}} 1&0&\small\frac{1}{2}\\ 0&1&\small-\frac{1}{2} \\ \end{array} \right] \\ \end{align*}$

Therefore, by Theorem VI.11, a basis for the row space is

$\textbf{w}_1=\left(1,0,\frac{1}{2}\right) \text{ and } \textbf{w}_2=\left(0,1,-\frac{1}{2}\right).$

To find a basis for the column space, the method is the same but with one added step. We must first find the transpose of our matrix [16].

The transpose of an $m\times n$ matrix $A$ is denoted as $A^T$ . Furthermore, the $i$ th row of $A$ is equal to the $i$ th column of $A^T$ , and the $j$ th column of $A$ is equal to the $j$ th row of $A^T$ for all $1\leq i\leq m$ and $1\leq j\leq n$ .

So, the transpose of our matrix is

$\left[ \begin{array}{@{}*{7}{r}@{}} 1&4\\ -3&2 \\ 2&1 \\ \end{array} \right]$

Converting to row-echelon form gives us

$\begin{align*} &\left[ \begin{array}{@{}*{7}{r}@{}} 1&4\\ -3&2 \\ 2&1 \\ \end{array} \right] &&\text{$3R_1+R_2\rightarrow R_2$ and $-2R_1+R_3\rightarrow R_3$}\\ &\left[ \begin{array}{@{}*{7}{r}@{}} 1&4\\ 0&14 \\ 0&-7 \\ \end{array} \right] &&\text{$\frac{1}{14} R_2\rightarrow R_2$} \\ &\left[ \begin{array}{@{}*{7}{r}@{}} 1&4\\ 0&1 \\ 0&-7 \\ \end{array} \right] &&\text{$7R_2+R_3\rightarrow R_3$} \\ &\left[ \begin{array}{@{}*{7}{r}@{}} 1&4\\ 0&1 \\ 0&0 \\ \end{array} \right] &&\text{$-4R_2+R_1\rightarrow R_1$} \\ &\left[ \begin{array}{@{}*{7}{r}@{}} 1&0\\ 0&1 \\ 0&0 \\ \end{array} \right] \end{align*}$

By Theorem VI.11, a basis for the row space of the transpose of our matrix is

$\textbf{w}_1=(1,0) \text{ and } \textbf{w}_2=(0,1).$

Because the rows of the transpose of our matrix are equal to the columns of our original matrix, the row space of the transpose of our matrix is equal to the column space of our original matrix. Therefore, a basis for the column space of our original matrix is the set of column vectors

$\begin{bmatrix} 1\\ 0 \end{bmatrix}\text{ and } \begin{bmatrix} 0\\ 1 \end{bmatrix}.$

So, we have seen row and column spaces and how to find a basis for each. Now, we will look at another type of space, the null space, and how to find a basis for this space.

31 Row and Column Spaces

License

Share This Book