1 Limits and Continuity
The idea of a limit is easy to understand if we have a graph. So, let’s begin by considering the graph of the function ![]() as is shown in Figure 1.
as is shown in Figure 1.
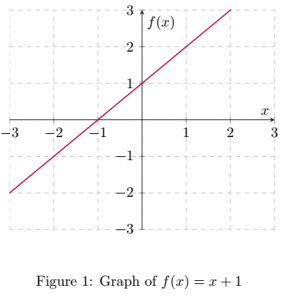
Let’s find the limit of ![]() as
as ![]() approaches 2. This is denoted as
approaches 2. This is denoted as
![]()
First, we trace along the graph of the function with our eyes or finger. Because we are finding the limit as ![]() approaches 2, we stop tracing when we reach the vertical line
approaches 2, we stop tracing when we reach the vertical line ![]() . Then, we follow the horizontal line from that point, where our function and the vertical line intersect, to the vertical axis. When we reach the vertical axis, we are at
. Then, we follow the horizontal line from that point, where our function and the vertical line intersect, to the vertical axis. When we reach the vertical axis, we are at ![]() so our final answer is
so our final answer is
![]()
This method not only works for continuous functions, but also discontinuous functions, as long as the one-sided limits are equal. We will discuss the ideas of continuity and one-sided limits in a moment. But first, we will discuss how to find limits analytically because a graph is not always available and may not work well as we will see in the next paragraph.
Let’s now find
![]()
We trace along the graph until we are at the point that intersects the vertical line at ![]() . We then follow the horizontal line from that intersection point to the vertical axis. In this case, it is not as clear what the equation of this horizontal line is. However, we do know that
. We then follow the horizontal line from that intersection point to the vertical axis. In this case, it is not as clear what the equation of this horizontal line is. However, we do know that ![]() so we can plug in
so we can plug in ![]() to find that
to find that
![]()
Therefore,
![]()
This second example gives us a glimpse into how we can find limits of continuous functions analytically as opposed to graphically. But before we dive deeper into the analytical method, we should introduce some properties of limits that will make the analytical process much easier. Larson and Edwards provide us with the following theorem [15].
Theorem I.1
Let ![]() and
and ![]() be real numbers, let
be real numbers, let ![]() be a positive integer, and let
be a positive integer, and let ![]() and
and ![]() be functions with the limits
be functions with the limits ![]() and
and ![]() .
.
- Scalar multiple:
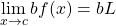
- Sum or difference:
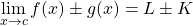
- Product:
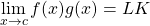
- Quotient:
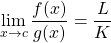
The proof of the difference rule is given in Part IV: Chapter 18, and the others can be proven in similar ways. The beauty of this theorem is that it allows us to easily find the limits of complicated functions analytically. Let’s look at a problem I completed for Calculus I that comes from Larson and Edwards [15].
Example 1
Find ![]() .
.
Solution
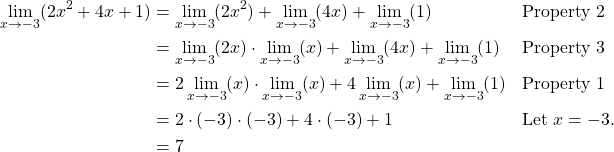
Up to this point, we have only been discussing continuous functions. Knowing whether a function is continuous or not is important when finding the limit because substituting directly as we did in this example does not always work with functions that are not continuous. So, what is a continuous function? A continuous function when graphed will have no holes or gaps. That is, it could be drawn without lifting up the pencil. However, since graphing each function is not the most efficient method, we must go a little deeper. Larson and Edwards provide us with the following formal definition for continuity [15].
A function ![]() is continuous at
is continuous at ![]() when these three conditions are met.
when these three conditions are met.
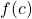 is defined.
is defined.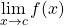 exists.
exists.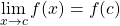 .
.
Let’s examine why the direct substitution method will not work when finding the limit of ![]() as
as ![]() approaches
approaches ![]() if
if ![]() is not continuous at
is not continuous at ![]() . That is, at least one of the above three conditions do not hold true for
. That is, at least one of the above three conditions do not hold true for ![]() .
.
If ![]() is not defined, plugging
is not defined, plugging ![]() into
into ![]() will result in an undefined value, such as
will result in an undefined value, such as ![]() .
.
Regarding the second condition, there are a couple of ways that the limit of ![]() as
as ![]() approaches
approaches ![]() might not exist. One is if the limit when approaching
might not exist. One is if the limit when approaching ![]() from the left does not equal the limit when approaching
from the left does not equal the limit when approaching ![]() from the right. This is denoted as
from the right. This is denoted as
![]()
Consider the following function.
As we can see from the graph,
![]()
Another reason the limit may not exist is if ![]() approaches infinity or negative infinity as
approaches infinity or negative infinity as ![]() approaches
approaches ![]() . This will occur when a function has a vertical asymptote at
. This will occur when a function has a vertical asymptote at ![]() . Because the function increases or decreases without limit as
. Because the function increases or decreases without limit as ![]() approaches
approaches ![]() , there is no limit.
, there is no limit.
Regarding the third condition, it is possible for the function to be defined at ![]() and for the limit at
and for the limit at ![]() to exist such that
to exist such that ![]() does not equal the limit at
does not equal the limit at ![]() . Consider the function
. Consider the function
![]()
As ![]() approaches 3 from the left or right,
approaches 3 from the left or right, ![]() approaches 3. So what we have is,
approaches 3. So what we have is,
![]()
Since we cannot use the direct substitution method, how do we find the limit of a function at ![]() when the function is not continuous at
when the function is not continuous at ![]() ? Well, we can find the left-sided limit by substituting a value that is a tiny bit smaller than
? Well, we can find the left-sided limit by substituting a value that is a tiny bit smaller than ![]() and the right-sided limit by substituting a value that is a tiny bit larger. If the one-sided limits are equal, then we have found the limit. Let’s look at a problem I completed for Calculus I that comes from Larson and Edwards [15].
and the right-sided limit by substituting a value that is a tiny bit larger. If the one-sided limits are equal, then we have found the limit. Let’s look at a problem I completed for Calculus I that comes from Larson and Edwards [15].
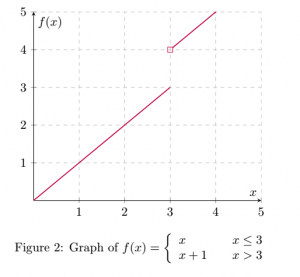
Let
![]()
Solution
Using the properties of Theorem I.1, we have
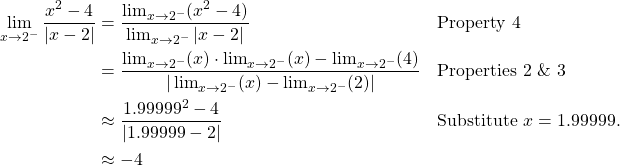
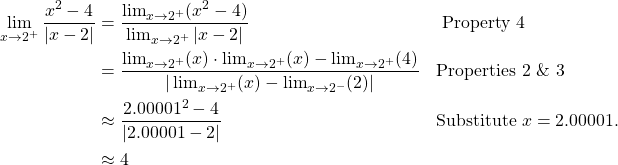
Because ![]() ,
, ![]() does not exist.
does not exist.
Now that we have discussed limits and continuity, we are ready to discuss one of the most important topics in Calculus, derivatives. The reason why we discussed these topics first is that derivatives cannot be defined without limits or even exist without continuity [15].
