10 Logic
We use logic every day in many areas of our lives. Logic is what enables us to determine whether an idea, belief, statement, etc. is true or false. As with any area of life, it is impossible for one idea to be true and at the same time false. This is known as the Law of Excluded Middle [23]. In mathematics, logic functions the same way. A mathematical statement is either true or false, and logic enables us to determine whether it is true or false. There are also different types of logical statements, which we will discuss below.
Disjunctions
In English, a disjunction can be identified by the word “or.” In math, we use the symbol ![]() to mean “or.” Suppose we have the following statements:
to mean “or.” Suppose we have the following statements:
![]()
![]()
If we want to combine these two statements to form a disjunction, then we have the following:
![]()
Using mathematical symbols, this statement is ![]() . Finding and creating disjunctions is not difficult. But we also need to determine whether a disjunction is true or false. This is where we use truth tables. The following is the truth table for disjunctions.
. Finding and creating disjunctions is not difficult. But we also need to determine whether a disjunction is true or false. This is where we use truth tables. The following is the truth table for disjunctions.
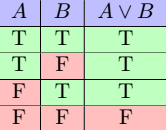
What this table is saying is that if ![]() ,
, ![]() , or
, or ![]() and
and ![]() are true, then the disjunction is true. The only way a disjunction can be false is if both
are true, then the disjunction is true. The only way a disjunction can be false is if both ![]() and
and ![]() are false.
are false.
By definition, an even number is one that is divisible by 2, and an odd number is one that is not. Because
![]()
7 is not divisible by two. Thus, seven is odd, but not even. So, our statement “seven is odd, or seven is even” is true because it is true that seven is odd even though it is not true that seven is even.
Conjunctions
In English, a conjunction can be identified by the word “and.” Sometimes “and” will actually be stated in the sentence while other times it will be implied. In math, we use the symbol ![]() to mean “and.” Suppose we have the following statements:
to mean “and.” Suppose we have the following statements:
![]()
![]()
If we want to combine these two statements to form a conjunction, then we have the following:
![]()
Using mathematical symbols, this statement is ![]() . The truth table is
. The truth table is
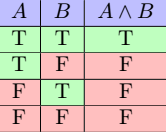
If ![]() ,
, ![]() , or
, or ![]() and
and ![]() are false, then the conjunction is false. The only way a conjunction can be true is if both
are false, then the conjunction is false. The only way a conjunction can be true is if both ![]() and
and ![]() are true. Because
are true. Because
![]()
6 is divisible by two but not five. Thus, our statement “six is divisible by two, and six is divisible by five” is false because it is false that six is divisible by five even though it is true that six is divisible by two.
Implications
In English, an implication can be identified by the word “if.” Suppose we have the following statements:
![]()
If we want to combine these two statements to form an implication, then we have the following: If there exists an integer ![]() that is divisible by 14, there exists an integer
that is divisible by 14, there exists an integer ![]() that is divisible by 7. Using mathematical symbols, this statement is
that is divisible by 7. Using mathematical symbols, this statement is ![]() . The truth table is
. The truth table is

An implication ![]() means that if
means that if ![]() is true then
is true then ![]() must be true. Thus, the only way an implication could be false is if
must be true. Thus, the only way an implication could be false is if ![]() is true but
is true but ![]() is not.
is not.
For an integer ![]() that is divisible by 14, we have
that is divisible by 14, we have
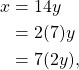
where ![]() is an integer.
is an integer.
Thus, if an integer is divisible by 14, it follows that this integer is also divisible by 7. Therefore, our statement “if there exists an integer ![]() that is divisible by 14, there exists an integer
that is divisible by 14, there exists an integer ![]() that is divisible by 7″ is true.
that is divisible by 7″ is true.
One additional symbol is ![]() , meaning “not,” which we will see in the following homework problem from Smith et al. that I completed for this paper [23].
, meaning “not,” which we will see in the following homework problem from Smith et al. that I completed for this paper [23].
Determine the truth value for each of the following.
- Although 51 divides 153, it is neither prime nor a divisor of 409.
- It is not the case that both -5 and 13 are elements of
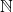 , but 4 is in the set of rational numbers.
, but 4 is in the set of rational numbers.
Solution
- Let statement
 be “51 divides 153,”
be “51 divides 153,” 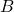 be “51 is prime,” and
be “51 is prime,” and 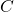 be “51 is a divisor of 409.” We will use a table to organize the information and help us reach the answer. Note that this is not a truth table as a truth table looks at all possible combinations of true and false. This table only looks at one combination, but it is all we need to solve the problem.
be “51 is a divisor of 409.” We will use a table to organize the information and help us reach the answer. Note that this is not a truth table as a truth table looks at all possible combinations of true and false. This table only looks at one combination, but it is all we need to solve the problem.

Therefore, the statement “although 51 divides 153, it is neither prime nor a divisor of 409″ is true.
- Let statement
 be “-5 is an element of
be “-5 is an element of 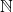 ,”
,” 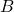 be “13 is an element of
be “13 is an element of 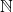 , and
, and 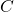 be “4 is in the set of rational numbers.”
be “4 is in the set of rational numbers.”
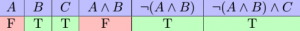
Therefore, the statement “it is not the case that both -5 and 13 are elements of
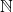 , but 4 is in the set of rational numbers” is true.
, but 4 is in the set of rational numbers” is true.
Next, we are going to take a quick look at a few logically equivalent statements, known as DeMorgan’s Laws.
DeMorgan’s Laws
DeMorgan’s Laws are simple, intuitive statements that give a couple rules of logic. They are stated as follows:
Theorem II.1 (DeMorgan’s Laws of Logic)
Let ![]() and
and ![]() be statements.
be statements.
One way of understanding what these laws are saying is to think of a multiple choice test. Suppose a question has options ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Now, suppose that we have eliminated option
. Now, suppose that we have eliminated option ![]() , we are saying that the answer is not
, we are saying that the answer is not ![]() and
and ![]() (
(![]() ). Because of this, we know that
). Because of this, we know that ![]() is not correct or
is not correct or ![]() is not correct (
is not correct (![]() ). That is the first law, and the second can be thought of in a similar way. Suppose we know that the answer is not
). That is the first law, and the second can be thought of in a similar way. Suppose we know that the answer is not ![]() or
or ![]() (
(![]() ). This leaves us with option
). This leaves us with option ![]() because it makes sense that when we say the answer is not
because it makes sense that when we say the answer is not ![]() or
or ![]() we mean that the answer is not
we mean that the answer is not ![]() and not
and not ![]() (
(![]() ).
).
The following example is one I wrote for this paper.
Write a statement that is equivalent to “Find an integer
Solution
Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() be the following statements respectively:
be the following statements respectively:
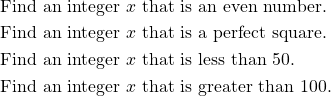
This means that the statement “find an integer ![]() that is an even number that is a perfect square” is
that is an even number that is a perfect square” is ![]() . It then follows that the statement “Find an integer
. It then follows that the statement “Find an integer ![]() that is not an even number that is a perfect square” is
that is not an even number that is a perfect square” is ![]() By the first of DeMorgan’s Laws,
By the first of DeMorgan’s Laws, ![]() . Thus, an equivalent statement to “find an integer
. Thus, an equivalent statement to “find an integer ![]() is not an even number that is a perfect square” would be “find an integer
is not an even number that is a perfect square” would be “find an integer ![]() that is either not an even number or not a perfect square.”
that is either not an even number or not a perfect square.”
The statement “find an integer ![]() that is less than 50 or greater than 100″ is
that is less than 50 or greater than 100″ is ![]() . It then follows that the statement “find an integer
. It then follows that the statement “find an integer ![]() that is not less than 50 or greater than 100″ is
that is not less than 50 or greater than 100″ is ![]()
By the second of DeMorgan’s Laws, ![]() . Thus, an equivalent statement to “find an integer
. Thus, an equivalent statement to “find an integer ![]() that is not less than 50 or greater than 100″ is “find an integer
that is not less than 50 or greater than 100″ is “find an integer ![]() that is not less than 50 and not greater than 100.”
that is not less than 50 and not greater than 100.”
Therefore, an equivalent statement to “find an integer ![]() that is not an even number that is a perfect square and is not less than 50 or greater than 100″ is “find an integer
that is not an even number that is a perfect square and is not less than 50 or greater than 100″ is “find an integer ![]() that is either not an even number or is not a perfect square and is not less than 50 and not greater than 100.”
that is either not an even number or is not a perfect square and is not less than 50 and not greater than 100.”
We have seen how DeMorgan’s laws can be applied to logic, but they are also used in set theory with slightly different notation. (See DeMorgan’s Laws in Part III: Chapter 13.) Additionally, these laws appear in other mathematical areas, such as discrete math and real analysis, and come in handy when constructing proofs, which we will now discuss.
