23 Groups
Most if not all topics discussed in modern algebra are connected to groups in some way. However, before we can understand what a group is, we must understand what a binary operation is. Fraleigh and Katz provide the following definition [7].
A binary operation
When a binary operation is a mapping from ![]() to
to ![]() , we say that
, we say that ![]() is closed under the binary operation.
is closed under the binary operation.
A binary operation is represented by ![]() , just as addition is represented by + and multiplication by
, just as addition is represented by + and multiplication by ![]() . Because addition and multiplication are themselves binary operations,
. Because addition and multiplication are themselves binary operations, ![]() will sometimes be used in place of + or
will sometimes be used in place of + or ![]() .
.
Now that we have a basic understanding of what a binary operation is, we are ready to look at the definition of a group as given by Fraleigh and Katz [7].
A group
- For all
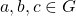 , we have
, we have
![Rendered by QuickLaTeX.com \[(a \ast b)\ast c=a\ast(b\ast c).\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6c2039a7b3eecb4189f2584d9314327e_l3.png)
- There is an element
 in
in 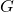 such that for all
such that for all 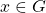 ,
,
![Rendered by QuickLaTeX.com \[e\ast x=x\ast e=x.\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a963dd91801fb0e448a7eb5ae955f031_l3.png)
- Corresponding to each
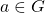 , there is an element
, there is an element 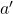 in
in 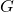 such that
such that
![Rendered by QuickLaTeX.com \[a\ast a'=a'\ast a=e.\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-af96db8a5d06a5338a60e6c1c96a9d32_l3.png)
A group ![]() is a specific type of set (see Part III: Chapter 13) that is closed under a binary operation
is a specific type of set (see Part III: Chapter 13) that is closed under a binary operation ![]() and must satisfy a few criteria. First, the binary operation must be associative. Second, the identity element of the binary operation is an element of
and must satisfy a few criteria. First, the binary operation must be associative. Second, the identity element of the binary operation is an element of ![]() . Third, every element in
. Third, every element in ![]() must have an inverse element that is also in
must have an inverse element that is also in ![]() .
.
So, to prove that a set ![]() is a group under a binary operation
is a group under a binary operation ![]() , we need to show that the group is closed under the operation and that the three conditions presented in the definition are satisfied. Let’s now look at an exercise from Fraleigh and Katz that I completed for this paper [7].
, we need to show that the group is closed under the operation and that the three conditions presented in the definition are satisfied. Let’s now look at an exercise from Fraleigh and Katz that I completed for this paper [7].
Let
Solution
Because every element in ![]() is the product of a positive integer and an integer, every element in
is the product of a positive integer and an integer, every element in ![]() is an integer because
is an integer because ![]() is closed under multiplication. So, for all
is closed under multiplication. So, for all ![]() ,
, ![]() because the distributive property holds in the integers. Because
because the distributive property holds in the integers. Because ![]() is closed under addition,
is closed under addition, ![]() Thus,
Thus,
![]()
and ![]() is closed under addition.
is closed under addition.
For all integers ![]() ,
,
![Rendered by QuickLaTeX.com \begin{align*} (a+b)+c &=a+(b+c) &&\text{Associativity holds in integers.}\\ n[(a+b)+c]&=n[a+(b+c)] &&\text{Multiply both sides by the integer $n$.} \\ n(a+b)+nc&=na+n(b+c) &&\text{Distributive property holds in integers.} \\ (na+nb)+nc&=na+(nb+nc) &&\text{Distributive property holds in integers.} \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1b72bf9598ad7160aa874eb91c537398_l3.png)
Thus, addition is associative for all elements ![]() .
.
For all integers ![]() ,
,

So, 0 is the identity element for ![]() under addition, and
under addition, and ![]() .
.
For all integers ![]() ,
,

For each ![]() ,
, ![]() is the additive inverse. Additionally,
is the additive inverse. Additionally, ![]() . Therefore,
. Therefore, ![]() is a group.
is a group.
There are many different types of groups. One is ![]() which we just saw is the set of all integers that are multiples of
which we just saw is the set of all integers that are multiples of ![]() . Another common group is
. Another common group is ![]() . Other types include cyclic, abelian, dihedral, alternating, and symmetric.
. Other types include cyclic, abelian, dihedral, alternating, and symmetric.
We are now going to look at subgroups, which are specific groups within a group. In particular, we will examine cyclic subgroups.
Cyclic Subgroups
Before we discuss what cyclic subgroups are, we need to understand what a subgroup is. It seems that a subgroup would be group within a group, similar to how a subset is a a set within a set. However, it is a little more complex than that. Fraleigh and Katz provide the following definition [7].
If a subset
If ![]() is a subgroup of a group
is a subgroup of a group ![]() under
under ![]() , it is also a subset of
, it is also a subset of ![]() . That is, every element in
. That is, every element in ![]() must also be in
must also be in ![]() . Additionally,
. Additionally, ![]() must be closed under the binary operation
must be closed under the binary operation ![]() and fulfill the three criteria given in definition V.2 for
and fulfill the three criteria given in definition V.2 for ![]() . We denote a subgroup as
. We denote a subgroup as ![]() . If we know that
. If we know that ![]() is not equal to
is not equal to ![]() ,
, ![]() is a proper subgroup denoted as
is a proper subgroup denoted as ![]() . Notice how the notation and terminology is very similar to that of sets (see Part III: Chapter 13).
. Notice how the notation and terminology is very similar to that of sets (see Part III: Chapter 13).
Now we are ready to discuss cyclic subgroups. Fraleigh and Katz provide the following definition [7].
Let
The notation of ![]() is a little misleading. We are not taking
is a little misleading. We are not taking ![]() to the power of
to the power of ![]() unless the binary operation is multiplication. For an element
unless the binary operation is multiplication. For an element ![]() of a group
of a group ![]() ,
, ![]() is actually equal to
is actually equal to ![]() , where
, where ![]() for all
for all ![]() and
and ![]() is the binary operation of
is the binary operation of ![]() .
.
There is another interesting aspect of these subgroups that Fraleigh and Katz give in the following theorem [7].
Theorem V.5
![]()
is a subgroup of ![]() and is the smallest subgroup of
and is the smallest subgroup of ![]() that contains
that contains ![]() , that is, every subgroup containing
, that is, every subgroup containing ![]() contains
contains ![]() .
.
Any subgroup ![]() of a group
of a group ![]() , defined under
, defined under ![]() , generated by an element
, generated by an element ![]() in
in ![]() , is the smallest subgroup containing
, is the smallest subgroup containing ![]() . That is, every subgroup containing
. That is, every subgroup containing ![]() contains
contains ![]() . Let’s take a moment to think through why this is true. Let
. Let’s take a moment to think through why this is true. Let ![]() be a subgroup of
be a subgroup of ![]() that contains
that contains ![]() . We have that
. We have that ![]() is mapped to
is mapped to ![]() by
by ![]() ,
, ![]() is mapped to
is mapped to ![]() by
by ![]() , and so on. Eventually, we will have
, and so on. Eventually, we will have ![]() is mapped to
is mapped to ![]() . Because
. Because ![]() is a subgroup,
is a subgroup, ![]() is closed. Because
is closed. Because ![]() contains
contains ![]() and is closed,
and is closed, ![]() is in
is in ![]() which implies
which implies ![]() is in
is in ![]() and so on. Thus,
and so on. Thus, ![]() is in
is in ![]() for all integers
for all integers ![]() . Because
. Because ![]() ,
, ![]() must contain
must contain ![]() .
.
Cyclic subgroups are helpful in that they make finding the smallest subgroup containing a specific element quite easy. Furthermore, we are guaranteed that the set of elements generated by an element ![]() is a subgroup of
is a subgroup of ![]() . Let’s look at an example that I created and completed for this paper. Recall that
. Let’s look at an example that I created and completed for this paper. Recall that ![]() is equal to the remainder when
is equal to the remainder when ![]() is divided by
is divided by ![]() .
.
Consider the group
![]()
with binary operation ![]() mod 9. Find the smallest subgroup that contains 3, denoted as
mod 9. Find the smallest subgroup that contains 3, denoted as ![]() .
.
Solution
By Theorem V.5, the smallest subgroup containing 3 would be the cyclic subgroup generated by 3.
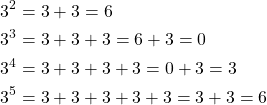
Since ![]() and
and ![]() both result in 6, we have found all of the elements of the set. If we keep going we will have a pattern of 0,3,6,0,3,6,… as
both result in 6, we have found all of the elements of the set. If we keep going we will have a pattern of 0,3,6,0,3,6,… as ![]() increases. Therefore, the smallest subgroup of
increases. Therefore, the smallest subgroup of ![]() containing 3 is
containing 3 is ![]()
We have seen how a subgroup, specifically a cyclic subgroup, relates to a group. Now, we are going to look at how groups relate to other groups through isomorphisms.
Isomorphisms
Let’s begin our discussion of isomorphishms by looking at the formal definition Fraleigh and Katz provide for us [7].
Let
![]()
Recall that in Part III: Chapter 15, we discussed one-to-one and onto functions. Now, suppose that we have such a function from one binary algebraic structure ![]() to another binary algebraic structure
to another binary algebraic structure ![]() . The fact that the function is one-to-one guarantees that each element in
. The fact that the function is one-to-one guarantees that each element in ![]() will be mapped to only one element in
will be mapped to only one element in ![]() . Because the function is onto, we are guaranteed that each element in
. Because the function is onto, we are guaranteed that each element in ![]() will be mapped to only one element in
will be mapped to only one element in ![]() . If we let
. If we let ![]() be the number of elements in
be the number of elements in ![]() and
and ![]() be the number of elements in
be the number of elements in ![]() , we have that
, we have that ![]() because the function is one-to-one and
because the function is one-to-one and ![]() because the function is onto. Thus,
because the function is onto. Thus, ![]() and
and ![]() must have the same number of elements. This gives us a glimpse into why isomorphisms are so important.
must have the same number of elements. This gives us a glimpse into why isomorphisms are so important.
When two binary algebraic structures ![]() and
and ![]() are isomorphic (
are isomorphic (![]() ), we say that they have the same structure, or structural properties. As we have seen, isomorphic binary algebraic structures have the same number of elements, though not necessarily the same elements [7]. Their binary operations would also have the same properties, such as being commutative, even if the binary operations themselves are not the same [7]. There are many more structural properties, but this provides the basic idea. If we can find an isomorphism from
), we say that they have the same structure, or structural properties. As we have seen, isomorphic binary algebraic structures have the same number of elements, though not necessarily the same elements [7]. Their binary operations would also have the same properties, such as being commutative, even if the binary operations themselves are not the same [7]. There are many more structural properties, but this provides the basic idea. If we can find an isomorphism from ![]() to
to ![]() , then we know all the structural properties are the same for
, then we know all the structural properties are the same for ![]() and
and ![]() .
.
Isomorphisms are of great importance because they help us study complex groups that are not very common and are more difficult to work with. Because two groups that are isomorphic have the exact same structural properties, isomorphisms allow us to find a simpler group with the same structural properties as a more complicated group [11]. Thus, structural properties of the complicated group can be discovered by way of the simpler one that otherwise may have gone undiscovered or taken much more effort to find.
To prove that two groups ![]() and
and ![]() are isomorphic, we must find a one-to-one mapping
are isomorphic, we must find a one-to-one mapping ![]() from
from ![]() onto
onto ![]() that satisfies
that satisfies
![]()
for all ![]() . We already discussed how to prove a mapping is one-to-one and onto in Part III: Chapter 15, and we can then use a direct proof (see Part II: Chapter 11) to show that
. We already discussed how to prove a mapping is one-to-one and onto in Part III: Chapter 15, and we can then use a direct proof (see Part II: Chapter 11) to show that
![]()
for all ![]() .
.
Before we complete the following example, we need to introduce one more definition so that what is done in the problem makes sense. This definition comes from Macauley [17].
The direct product of groups
![]()
Now we are ready to begin our example which is a homework problem I completed for Modern Algebra [18].
Let
Show that
![]()
where ![]() with multiplication as the binary operation.
with multiplication as the binary operation.
Proof.
Let ![]() be defined as
be defined as ![]()
To prove that ![]() is one-to-one, we need to show that if
is one-to-one, we need to show that if ![]() then
then ![]() . We will show this by proving two cases.
. We will show this by proving two cases.
Case 1: Let ![]()
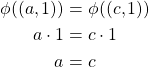
Case 2: Let ![]() .
.
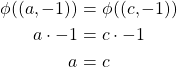
Thus, ![]() is one-to-one. To prove that
is one-to-one. To prove that ![]() is onto, we need to show that for each
is onto, we need to show that for each ![]() , there exists
, there exists ![]() such that
such that ![]() . We will show this by proving two cases as well.
. We will show this by proving two cases as well.
Case 1: Let ![]() be in
be in ![]()
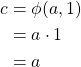
Case 2: Let ![]() be in
be in ![]() .
.
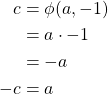
Thus, ![]() is onto.
is onto.
Finally, for all ![]() and
and ![]() ,
,

Because ![]() is a one-to-one mapping from
is a one-to-one mapping from ![]() onto
onto ![]() and
and
![]()
holds for all ![]() and
and ![]() ,
,
![]()
Isomorphisms will come up again later when we discuss factor groups, which are groups made up of cosets. So, let’s find out what cosets are.
Cosets
Cosets are derived from an element of a group ![]() and a subgroup of
and a subgroup of ![]() . Let’s examine the following definition provided by Fraleigh and Katz [7].
. Let’s examine the following definition provided by Fraleigh and Katz [7].
Let
For a group ![]() under a binary operation
under a binary operation ![]() and a subgroup
and a subgroup ![]() of
of ![]() , if we take an element
, if we take an element ![]() of
of ![]() and perform the binary operation on
and perform the binary operation on ![]() and every element in
and every element in ![]() , the resulting set of elements is known as a coset. As not every binary operation is commutative,
, the resulting set of elements is known as a coset. As not every binary operation is commutative, ![]() is not necessarily equal to
is not necessarily equal to ![]() , where
, where ![]() is an element of
is an element of ![]() . The elements of the form
. The elements of the form ![]() make up the left coset of
make up the left coset of ![]() containing
containing ![]() , denoted as
, denoted as ![]() , because
, because ![]() is to the left of
is to the left of ![]() . Similarly, the elements
. Similarly, the elements ![]() make up the right coset
make up the right coset ![]() because
because ![]() is to the right of
is to the right of ![]() .
.
Another interesting fact of left cosets is that they partition the group ![]() [7]. That is, if we take the union of all of the left cosets, we will get the entire group
[7]. That is, if we take the union of all of the left cosets, we will get the entire group ![]() . Additionally, none of the left cosets have an element in common. That is, the intersection of the left cosets is the empty set.
. Additionally, none of the left cosets have an element in common. That is, the intersection of the left cosets is the empty set.
We could also replace “left” with “right” in the preceding paragraph and still get true statements. (Refer back to Part III: Chapter 13 for a review of the terms union, intersection, and empty set.)
Let’s now try to find all of the cosets of a subgroup. The following example is an exercise from Fraleigh and Katz that I completed for this paper [7].
Find all cosets of the subgroup
![]()
with the binary operation ![]() mod(12).
mod(12).
Solution
The subgroup ![]() is the cyclic subgroup generated by 4.
is the cyclic subgroup generated by 4.
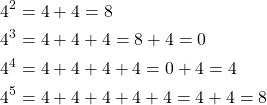
If we continue on, we will have a pattern of 0,4,8,0,4,8,…. So,
![]()
The left cosets are then:
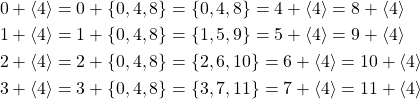
and the right cosets are:
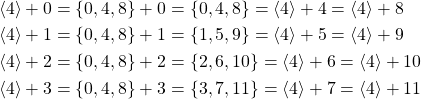
Because the right cosets are identical to the left cosets, the cosets of the subgroup ![]() of
of ![]() are
are ![]() and
and ![]() .
.
Notice how none of the left cosets have an element in common. Additionally, every element of ![]() appears in one of these left cosets. The same is true for the right cosets. This is what it means to say that the left or right cosets partition the group that they are subsets of. This now brings us to the Theorem of Lagrange which is developed from this idea that cosets partition the group.
appears in one of these left cosets. The same is true for the right cosets. This is what it means to say that the left or right cosets partition the group that they are subsets of. This now brings us to the Theorem of Lagrange which is developed from this idea that cosets partition the group.
Theorem of Lagrange
This theorem is stated by Fraleigh and Katz as follows, and the proof is one I wrote based off of the proof given by Fraleigh and Katz [7].
Theorem V.9 (Theorem of Lagrange)
Proof.
The order of a group is simply the number of elements in the group. So, what we need to show is that the number of elements in ![]() is a divisor of the number of elements in
is a divisor of the number of elements in ![]() .
.
We have that every left (or right) coset of ![]() has the same number of elements as
has the same number of elements as ![]() . Because the union of the left cosets is
. Because the union of the left cosets is ![]() and their intersection is the empty set, we have
and their intersection is the empty set, we have
![]()
where ![]() and
and ![]() are the orders of
are the orders of ![]() and
and ![]() respectively. Thus,
respectively. Thus, ![]() for some
for some ![]() . Therefore,
. Therefore, ![]() is a divisor of
is a divisor of ![]() .
.
The contrapositive (see Part II: Chapter 11) of this theorem is true. That is, any subset ![]() of a group
of a group ![]() with an order that is not a divisor of the order of
with an order that is not a divisor of the order of ![]() is not a subgroup of
is not a subgroup of ![]() . However, the converse of this theorem is not true. If the order of
. However, the converse of this theorem is not true. If the order of ![]() is a divisor of the order of
is a divisor of the order of ![]() , it does not necessarily follow that
, it does not necessarily follow that ![]() is a subgroup of
is a subgroup of ![]() .
.
Let’s look at an example that I wrote that puts these ideas into practice.
Consider the group
![]()
under addition modulo 16. Are the sets
![]()
and
![]()
subgroups of ![]() ?
?
Solution
We have that
![]()
Because the order of ![]() is 6 and the order of
is 6 and the order of ![]() is 16,
is 16, ![]() is not a subgroup of
is not a subgroup of ![]() by the Theorem of Lagrange.
by the Theorem of Lagrange.
Additionally, we have that
![]()
Because the order of ![]() is 8 and the order of
is 8 and the order of ![]() is 16, the Theorem of Lagrange is inconclusive.
is 16, the Theorem of Lagrange is inconclusive.
By definition V.3, ![]() is a subgroup of
is a subgroup of ![]() if and only if it is a subset of
if and only if it is a subset of ![]() that is a group under the binary operation of
that is a group under the binary operation of ![]() . Because every element in
. Because every element in ![]() is in
is in ![]() , it is a subset. However, the identity element for addition modulo 16 is 0, which is not an element of
, it is a subset. However, the identity element for addition modulo 16 is 0, which is not an element of ![]() . Thus,
. Thus, ![]() is not a group under the binary operation of
is not a group under the binary operation of ![]() . Therefore,
. Therefore, ![]() is not a subgroup of
is not a subgroup of ![]() .
.
We have seen how the Theorem of Lagrange grew from the idea of cosets. Now, we are going to discuss another topic that would not be possible without cosets, factor groups.
Factor Groups
A factor group is ![]() where
where ![]() is a subgroup of
is a subgroup of ![]() [7]. Because the elements of
[7]. Because the elements of ![]() are just the left cosets of
are just the left cosets of ![]() , we are more concerned with finding what group a factor group is isomorphic to than we are with finding what the actual elements of a factor group are.
, we are more concerned with finding what group a factor group is isomorphic to than we are with finding what the actual elements of a factor group are.
To compute a factor group is to find a group that the factor group is isomorphic to [7]. The best way to understand how to compute a factor group is to see an example so we will work through one now. This is a homework problem that I completed for this paper that comes from Fraleigh and Katz [7].
Compute the factor group
Solution
We first need to show that ![]() is a subgroup of
is a subgroup of ![]() . By definition V.3,
. By definition V.3, ![]() must be a group under the binary operation of
must be a group under the binary operation of ![]() . We are given that both
. We are given that both
![]() and
and ![]() are defined under addition. Moreover, they are both groups under addition by example 49. All that remains left to show is that every element of
are defined under addition. Moreover, they are both groups under addition by example 49. All that remains left to show is that every element of ![]() is in
is in ![]() . That is, we need to show that any integer that is a multiple of 8 is also a multiple of 2. We have that for an element
. That is, we need to show that any integer that is a multiple of 8 is also a multiple of 2. We have that for an element ![]() ,
,
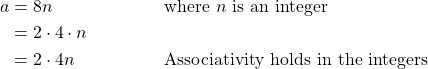
Because ![]() and 4 are integers and the integers are closed under multiplication,
and 4 are integers and the integers are closed under multiplication, ![]() is an integer. Thus, if an integer is a multiple of 8, it is also a multiple of 2. Therefore, we can conclude that
is an integer. Thus, if an integer is a multiple of 8, it is also a multiple of 2. Therefore, we can conclude that ![]() is a subgroup of
is a subgroup of ![]() .
.
Now, we need to find all left cosets of the subgroup ![]() of
of ![]() . Because
. Because ![]() is the group of all integers that are multiples of 2, we need to add
is the group of all integers that are multiples of 2, we need to add ![]() to every even integer to get the left cosets. We have then
to every even integer to get the left cosets. We have then

where ![]() . So, we have that
. So, we have that
![]()
which is a group under the binary operation
![]()
Because ![]() has four elements, we know that any group isomorphic to it must have four elements as well. This is because an isomorphism is a one-to-one, onto mapping, which means that there is a one-to-one correspondence between the elements of the domain and codomain (see Part III: Chapter 15). Thus, the domain and codomain (when they are finite) have the same number of elements. One group that has four elements is
has four elements, we know that any group isomorphic to it must have four elements as well. This is because an isomorphism is a one-to-one, onto mapping, which means that there is a one-to-one correspondence between the elements of the domain and codomain (see Part III: Chapter 15). Thus, the domain and codomain (when they are finite) have the same number of elements. One group that has four elements is ![]() with the binary operation
with the binary operation
![]()
Now, we need to see if we can find an isomorphism ![]() from
from ![]() to
to ![]() . Let
. Let ![]() It is easy to show that
It is easy to show that ![]() is one-to-one and onto.
is one-to-one and onto.
One-to-One
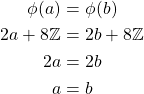
Onto
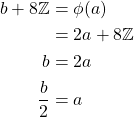
Additionally, we have
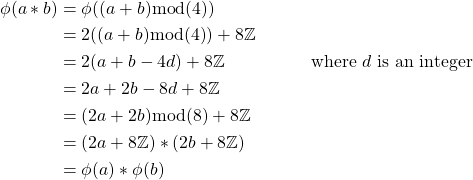
Therefore, ![]() is isomorphic to
is isomorphic to ![]() .
.
We have now seen two examples of how to find an isomorphism, each one demonstrating how long this process can be. Thankfully, we do have some shortcuts, such as the FTFGAG.
FTFGAG
FTFGAG stands for the Fundamental Theorem of Finitely Generated Abelian Groups. This theorem is given by Macauley as follows [17].
Theorem V.10 (FTFGAG)
![]()
where each ![]() is a prime power, i.e.,
is a prime power, i.e., ![]() , where
, where ![]() is prime and
is prime and ![]() .
.
There are a couple terms in this theorem that we have not yet covered. A group ![]() under
under ![]() is abelian if and only if
is abelian if and only if ![]() is commutative for all elements in
is commutative for all elements in ![]() . A group
. A group ![]() is cyclic if and only if there exists an element in
is cyclic if and only if there exists an element in ![]() that generates all of
that generates all of ![]() [17]. For example,
[17]. For example, ![]() is cyclic for all natural numbers
is cyclic for all natural numbers ![]() because
because
![]()
So, every finite abelian group is isomorphic to a direct product of cyclic groups. More specifically, the cyclic groups are of the form ![]() where
where ![]() is a prime number raised to some power. Let’s demonstrate this using an example. This exercise is a homework problem I completed for Modern Algebra [18].
is a prime number raised to some power. Let’s demonstrate this using an example. This exercise is a homework problem I completed for Modern Algebra [18].
List every direct product of cyclic groups that is isomorphic to an abelian group of order 54.
Solution
Finite isomorphic groups have the same order because an isomorphism is a one-to-one, onto mapping (see Part III: Chapter 15). Because the order of ![]() is equal to
is equal to ![]() , we need to find every combination of products of primes to some power that equal 54. Because
, we need to find every combination of products of primes to some power that equal 54. Because ![]() , we have the following combinations:
, we have the following combinations:
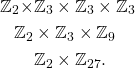
Therefore, every finite abelian group of order 54 is isomorphic to one of these direct products of cyclic groups by the FTFGAG.
Listing out all of the possible direct products becomes a long task when an abelian group is of an order that is the product of many primes. But if we only need to find one group that is isomorphic to a particular abelian group, this theorem is extremely useful.
We have covered a good amount of information relating to the algebraic binary structure known as a group. We covered cyclic subgroups, isomorphisms, cosets, and factor groups. We also discussed a couple of important and useful theorems, the Theorem of Lagrange and the FTFGAG. We are now going to turn our attention to other types of algebraic binary structures. These are rings, integral domains, and fields.
