18 Axioms of the Real Numbers
Axioms of the real numbers are statements that describe the qualities and properties that the real numbers possess. We are going to cover the field axioms and then the triangle inequality.
Field Axioms
A field is a set that satisfies the field axioms given in the definition below, which comes from Abbott [1].
A set ![]() is a field if there exist two operations, addition
is a field if there exist two operations, addition ![]() and multiplication
and multiplication ![]() , that satisfy the following list of conditions:
, that satisfy the following list of conditions:
- (Commutativity)
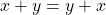 and
and 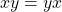 for all
for all 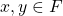 .
. - (Associativity)
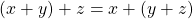 and
and 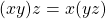 for all
for all 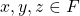 .
. - (Identities exist) There exist two special elements 0 and 1 with
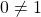 such that
such that 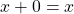 and
and 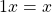 for all
for all 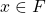 .
. - (Inverses exist) Given
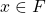 , there exists an element
, there exists an element 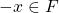 such that
such that 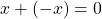 . If
. If 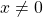 , there exists an element
, there exists an element 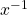 such that
such that 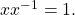
- (Distributive property)
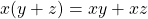 for all
for all 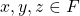 .
.
Basically, a set is a field if and only if the commutative and associative properties hold for all of the elements under addition and multiplication, the distributive property of multiplication holds, the set contains identity elements for addition and multiplication, and the inverses of each element under addition and multiplication are also elements of the set. We have already been working with fields without even realizing it. The set of rational numbers and the set of real numbers are both fields.They are also ordered fields, which are fields that must satisfy the following additional properties [1].
- For any two elements
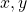 in a set
in a set 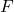 , either
, either 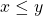 or
or 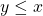 .
. - If
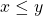 and
and 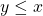 , then
, then 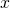 must equal
must equal 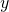 .
. - If
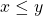 and
and 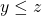 , then
, then 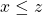 .
. - If
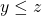 , then
, then 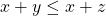 .
. - If
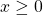 and
and 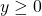 , then
, then 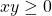 .
.
Looking at these properties, it becomes clear why we refer to fields satisfying them as ordered fields. These properties ensure that there is a specific order preserved throughout the field.
Let’s now look at a few well known sets and determine whether they are fields. The following exercise is a homework problem from Abbott that I completed for this paper [1].
Determine whether the sets
First off, we know that the commutative, associative, and distributive properties all hold for these sets.Regarding the natural numbers, for
![]()
but -5 is not a natural number. Thus, ![]() is not a field.Regarding the integers, for
is not a field.Regarding the integers, for ![]() ,
, ![]() . That is, the multiplicative identity is 1. However, multiplicative inverses do not exist within the integers. For example,
. That is, the multiplicative identity is 1. However, multiplicative inverses do not exist within the integers. For example,
![]()
but ![]() is not an integer. Thus,
is not an integer. Thus, ![]() is not a field.Regarding the rational numbers, for
is not a field.Regarding the rational numbers, for ![]() ,
,
![]()
Since 0, 1, ![]() , and
, and ![]() for all rational numbers
for all rational numbers ![]() are themselves elements of the rational numbers,
are themselves elements of the rational numbers, ![]() is a field. Furthermore,
is a field. Furthermore, ![]() is an ordered field because the five properties listed above are satisfied for all
is an ordered field because the five properties listed above are satisfied for all ![]() .
.
Later on, we will revisit the idea of fields in Part V: Chapter 24 when we are discussing Modern Algebra. But for now, we are going to move on to a simple but powerful axiom of the real numbers known as the triangle inequality.
Triangle Inequality
The triangle inequality is stated by Abbott as follows [1]:
![]()
where ![]() and
and ![]() are real numbers.
are real numbers.
Much like the Pigeonhole Principle (see Part III: Chapter 16), the triangle inequality is a simple statement that helps us prove many more complex ideas.
Recall that in Part I: Chapter 1, we discussed some properties of limits that made it easier to solve limits analytically. We will now present the proof for the property
![]()
where ![]() and
and ![]() . To prove this, we will be using definition IV.20 as given in chapter 21.
. To prove this, we will be using definition IV.20 as given in chapter 21.
The following proof is a homework problem from Abbott that I completed for Introduction to Analysis [1].
Show that
![]()
where ![]() and
and ![]() .
.
Using the triangle inequality, we have
![]()
Let ![]() . By definition IV.20, there exists
. By definition IV.20, there exists ![]() such that if
such that if ![]() ,
,
![]()
By definition IV.20, there also exists ![]() such that if
such that if ![]() ,
,
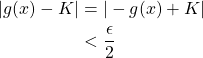
Let ![]() If
If ![]() ,
,
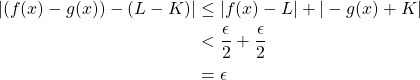
Therefore,
![]()
by definition IV.20.
This is just one example of how useful the triangle inequality is. There is so much that we would not be able to prove without it. But time is precious, and we must move on to the topology of the real numbers, which contains some of the most interesting ideas covered in analysis.
