16 Cardinality
Cardinality deals with the number of elements in a set. Based on the number of elements in a set, we can categorize it as either finite or infinite. If it is infinite, we can further categorize it as countable (denumerable) or uncountable.
Smith et al. tells a story of a shepherd with more sheep than he is able to count. Because the shepherd needs to know whether some sheep are missing or not, he devises a method that enables him to keep track without having to count them. He has a pebble for each sheep. As they come in one by one, he moves pebbles from one container to another one by one. If not all of the pebbles have been transferred over, he knows that he is missing some sheep [23].
In the story, the shepherd used a one-to-one correspondence between the pebbles and the sheep. When working with very large sets, the elements are like the sheep and the natural numbers, the pebbles. In other words, we form a one-to-one correspondence between the natural numbers and the elements of a set to determine the cardinality of a finite set.
Finite Sets
Equivalence
Using the ideas of one-to-one and onto functions, we can determine whether two finite sets are equivalent. This is not the same as equal. When two sets are equal, they have the exact same elements. Let’s look at the definition of equivalent sets from Smith et al. [23].
Two sets
Recall that when we have a one-to-one function that we have a one-to-one correspondence between the elements of the domain and the elements of the range. An onto function is one where the range and codomain are equal sets. Combining these two ideas together, two sets are equivalent if there exists a function ![]() where the elements of the domain have a one-to-one correspondence to the elements of the codomain. When referring to finite sets, the domain must have the same number of elements as the codomain. Let’s look at a problem that I have written and completed for this paper.
where the elements of the domain have a one-to-one correspondence to the elements of the codomain. When referring to finite sets, the domain must have the same number of elements as the codomain. Let’s look at a problem that I have written and completed for this paper.
Show that the sets
![]()
and
![]()
are equivalent.
Proof.
We need to find a function ![]() that is one-to-one and onto
that is one-to-one and onto ![]() . Just looking at the sets, it seems that we can define a function
. Just looking at the sets, it seems that we can define a function ![]() as
as
![]()
Now we need to show that ![]() is one-to-one and onto
is one-to-one and onto ![]() . Let
. Let ![]() . It follows that
. It follows that
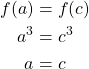
Thus, ![]() is one-to-one. Now, we need to show that
is one-to-one. Now, we need to show that ![]() is onto by showing that for every
is onto by showing that for every ![]() in
in ![]() there exists an
there exists an ![]() in
in ![]() such that
such that ![]() So, we have that
So, we have that
![Rendered by QuickLaTeX.com \begin{align*} b&=f(a)\\ &=a^3\\ \sqrt[3]{b}&=a\\ \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1bc057e4948f84e322d41755f8368be7_l3.png)
Since for each element ![]() there exists an element
there exists an element ![]() such that
such that ![]() ,
, ![]() is onto. Therefore, the sets
is onto. Therefore, the sets ![]() and
and ![]() are equivalent.
are equivalent.
Now that we understand what equivalent sets are, we are ready to discuss the idea of cardinality.
Cardinality
Let’s begin with a couple more definitions from Smith et al. [23].
For each natural number
Definition III.11
Let ![]() be a finite set.
be a finite set.
- If
 , then
, then  has cardinal number 0 (or cardinality 0). We write
has cardinal number 0 (or cardinality 0). We write  .
. - If
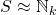 for some natural number
for some natural number 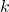 , then
, then 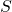 has cardinal number
has cardinal number 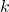 (or cardinality
(or cardinality 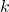 ), and we write
), and we write  .
.
Simply, the cardinal number of a finite set is the number of elements in the set. Let’s look at another example that I wrote for this paper.
Example 35
Consider the sets
![]()
and
![]()
Show that ![]() is a finite set and find its cardinality.
is a finite set and find its cardinality.
Solution
Using the same method that we used in example 34, we know that ![]() and
and ![]() are equivalent sets because we have a function
are equivalent sets because we have a function ![]() defined as
defined as
![]()
that is a one-to-one function onto ![]() .
.
Notice that ![]() which implies that
which implies that ![]() So, by definitions III.10 and III.11, we know that
So, by definitions III.10 and III.11, we know that ![]() is a finite set with cardinality 5.
is a finite set with cardinality 5.
This now brings us to the Pigeonhole Principle, a statement that is so intuitive yet so powerful.
Pigeonhole Principle
The Pigeonhole Principle is stated by Smith et al. as follows [23].
Theorem III.12 (Pigeonhole Principle)
As this is called the pigeonhole principle, we will use pigeons and pigeonholes to help visualize what this is saying. Let ![]() be the number of pigeons and
be the number of pigeons and ![]() be the number of pigeonholes. Let
be the number of pigeonholes. Let ![]() be the function of placing a pigeon into a pigeonhole. If the number of pigeons is greater than the number of pigeonholes, then at least one pigeonhole will contain more than one pigeon. Thus, there is not a one-to-one correspondence between pigeons and pigeonholes.
be the function of placing a pigeon into a pigeonhole. If the number of pigeons is greater than the number of pigeonholes, then at least one pigeonhole will contain more than one pigeon. Thus, there is not a one-to-one correspondence between pigeons and pigeonholes.
Smith et al. also provides the following corollary that comes from this principle [23].
Corollary III.12.1
What this corollary is saying is that if the domain has more elements than the codomain, then it is not possible for a one-to-one mapping from the domain to the codomain to exist. This is because there will be at least two elements in the domain that map to the same element in the codomain, which is not a one-to-one mapping.Let’s now look at an exercise from Smith et al. that I completed for this paper [23].
An English market town has a population of 21,307. Assuming that every resident has a first, middle, and last name, show that there are two residents with identical three-letter initials.
Proof.
Because there are 26 letters in the English alphabet, there are ![]() possible combinations for an individual’s initials. Let
possible combinations for an individual’s initials. Let ![]() be the set of residents and
be the set of residents and ![]() be the set of possible initials. Because
be the set of possible initials. Because ![]() ,
, ![]() , and
, and ![]() , there is no one-to-one mapping from
, there is no one-to-one mapping from ![]() to
to ![]() by Corollary III.12.1. That is, there exist two people who are mapped to the same initials. Therefore, there are two residents with identical three-letter initials.
by Corollary III.12.1. That is, there exist two people who are mapped to the same initials. Therefore, there are two residents with identical three-letter initials.
We have seen that the cardinality of a finite set is the number of elements contained in that set, but how does cardinality apply to infinite sets? That is what we are about to find out.
Infinite Sets
Denumerable Sets
An infinite set is simply a set that is not finite. Each infinite set is either denumerable or uncountable. Smith et al. provides the following definition for a denumerable set [23].
The set
What this is saying is that an infinite set ![]() is denumerable if there is a one-to-one correspondence between the elements of
is denumerable if there is a one-to-one correspondence between the elements of ![]() and the natural numbers.
and the natural numbers.
For example, the set of positive rational numbers is an infinite set that is denumerable, though intuitively it may seem otherwise. Georg Cantor devised a clever way for showing that the positive rational numbers have a one-to-one correspondence with the natural numbers and thus proved that the positive rational numbers are denumerable.
Proof.
We will use the following image taken from Smith et al. to explain the method Cantor used.

Start by writing the positive rational numbers in a matrix as shown above. The first row contains all positive rationals with a denominator of one, the second row contains all those with a denominator of two, and so on. The first column contains all positive rationals with a numerator of one, the second column contains all those with a numerator of two, and so on.
Then, draw diagonals in the manner that is shown above and create the one-to-one mapping below by following the diagonals and leaving out any duplicates (such as ![]() and
and ![]() since they are equal to
since they are equal to ![]() ). This image is also taken from Smith et al.
). This image is also taken from Smith et al.

As there is a one-to-one correspondence between the natural numbers and positive rational numbers, the positive rationals are denumerable.
Building off of the idea of denumerable sets, we have countable and uncountable sets. A countable set is not necessarily infinite, but a denumerable set is always countable, as we will see.
Countable and Uncountable Sets
The formal definitions of countable and uncountable sets are given by Smith et al. as follows [23].
A set
We have seen that the positive rational numbers are denumerable and consequently, countable. But what about the interval of real numbers (0,1)? It may be surprising to know that this interval is uncountable, which was also proved by Cantor. The key to the proof is in showing that there is not a one-to-one correspondence between the natural numbers and this set of real numbers. It then follows that this infinite set is not denumerable and thus, uncountable. So, let’s look at how Cantor proved that ![]() is not denumerable [19].
is not denumerable [19].
Proof.
Let ![]() be a function such that
be a function such that ![]() . Let
. Let ![]() be a natural number and consider the following table.
be a natural number and consider the following table.
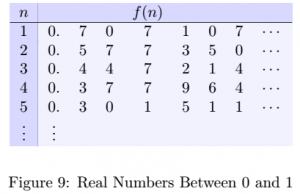
The first row is the decimal expansion of ![]() . The second row is the decimal expansion of
. The second row is the decimal expansion of ![]() , and the third is
, and the third is ![]() . The fourth is
. The fourth is ![]() , and the fifth is
, and the fifth is ![]() . The table continues on and on where the
. The table continues on and on where the ![]() row is the decimal expansion of
row is the decimal expansion of ![]() , where
, where ![]()
What we want to determine is if ![]() is onto. That is, can every possible real number between 0 and 1 be placed in the table? Well, consider the same table where the digits along one of the diagonals are in bold.
is onto. That is, can every possible real number between 0 and 1 be placed in the table? Well, consider the same table where the digits along one of the diagonals are in bold.
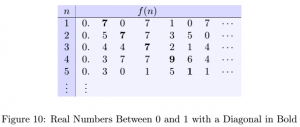
Let’s add one to each of those bolded numbers and get a new decimal number, 0.88802…. Could this number be in the table somewhere? Well, this number cannot be equal to ![]() because its first digit is one added to the first digit of
because its first digit is one added to the first digit of ![]() . Similarly, this number cannot be equal to
. Similarly, this number cannot be equal to ![]() because its second digit is one added to the second digit of
because its second digit is one added to the second digit of ![]() . This continues on so that this number cannot equal
. This continues on so that this number cannot equal ![]() because its
because its ![]() digit is one added to the
digit is one added to the ![]() digit of
digit of ![]() So, there does not exist an
So, there does not exist an ![]() in the domain of
in the domain of ![]() such that
such that ![]() .
.
This is not the only number that cannot be in the table. Any number we create by changing the digits along a diagonal will result in a number that cannot be in the table by similar reasoning. Thus, ![]() is not onto which implies that the set of all real numbers in the open interval (0,1) is not equivalent to the set of natural numbers. By Definition III.13, (0,1) is not denumerable. Since (0,1) is neither finite nor denumerable, it is uncountable by Definition III.14.
is not onto which implies that the set of all real numbers in the open interval (0,1) is not equivalent to the set of natural numbers. By Definition III.13, (0,1) is not denumerable. Since (0,1) is neither finite nor denumerable, it is uncountable by Definition III.14.
