33 Eigenvalues
Eigenvalues are very important and have many applications. (A couple of which are studying population growth and solving certain types of differential equations seen in engineering and science [16].) They have grown from the need to solve the eigenvalue problem.
Larson and Falvo give the following statement for the eigenvalue problem: “If ![]() is an
is an ![]() matrix, do there exist
matrix, do there exist ![]() nonzero matrices x such that
nonzero matrices x such that ![]() is a scalar multiple of x?” [16]. Note that the eigenvalue problem only applies to
is a scalar multiple of x?” [16]. Note that the eigenvalue problem only applies to ![]() matrices.
matrices.
The scalar is denoted as ![]() and is called the eigenvalue, and x is the eigenvector [16]. So, what we want to know is what eigenvalues and eigenvectors satisfy the equation
and is called the eigenvalue, and x is the eigenvector [16]. So, what we want to know is what eigenvalues and eigenvectors satisfy the equation
![]()
which can be rewritten as
![]()
To find the eigenvalues, we solve the characteristic equation
![]()
for ![]() . This is because the homogeneous equation
. This is because the homogeneous equation ![]() has a nonzero solution only if the determinant of
has a nonzero solution only if the determinant of ![]() is equal to zero [16]. In other words, we want to find
is equal to zero [16]. In other words, we want to find ![]() such that
such that ![]() has a nonzero solution. After finding
has a nonzero solution. After finding ![]() , we use the equation
, we use the equation
![]()
where 0 is the zero vector, to find the corresponding eigenvector. Note that we do not let x equal zero because ![]() is just the trivial solution [16]. Let’s now look at an example that I completed for Elementary Linear Algebra that comes from Larson and Falvo [16].
is just the trivial solution [16]. Let’s now look at an example that I completed for Elementary Linear Algebra that comes from Larson and Falvo [16].
Find the the eigenvalues and the corresponding eigenvectors for
Solution
Using the characteristic equation and solving for ![]() , we have
, we have
![Rendered by QuickLaTeX.com \begin{align*} 0&= \left|\lambda\begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}+ (-1)\left[ \begin{array}{@{}*{7}{r}@{}} -2&4\\ 2&5 \\ \end{array} \right]\right|\\ &=\left|\begin{bmatrix} \lambda&0\\ &\lambda \end{bmatrix}+\left[ \begin{array}{@{}*{7}{r}@{}} 2&-4\\ -2&-5 \\ \end{array} \right]\right|\\ &=\left|\left[ \begin{array}{@{}*{7}{r}@{}} \lambda+2&-4\\ -2&\lambda -5 \\ \end{array} \right]\right|\\ &=(\lambda+2)(\lambda-5)-(-2)(-4)\\ &=\lambda^2-3\lambda-18\\ &=(\lambda+3)(\lambda-6)\\ \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-24212f6b542545c3059b359dd71165c8_l3.png)
This implies that ![]() equals -3 or 6. To find the corresponding eigenvectors, we have to solve
equals -3 or 6. To find the corresponding eigenvectors, we have to solve ![]() for x when
for x when ![]() and when
and when ![]() For
For ![]() ,
,
![Rendered by QuickLaTeX.com \begin{align*} \lambda I-A&=-3\begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}+ (-1)\left[ \begin{array}{@{}*{7}{r}@{}} -2&4\\ 2&5 \\ \end{array} \right]\\ &=\left[ \begin{array}{@{}*{7}{r}@{}} -3&0\\ 0&-3 \\ \end{array} \right]+ \left[ \begin{array}{@{}*{7}{r}@{}} 2&-4\\ -2&-5 \\ \end{array} \right]\\ &=\left[ \begin{array}{@{}*{7}{r}@{}} -1&-4\\ -2&-8 \\ \end{array} \right] \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-84b7274237da0acb04c18dbf7eae9891_l3.png)
Using elementary row operations, we get ![]()
The solutions to the equation
![]()
which can be written as
![]()
are ![]() matrices that satisfy
matrices that satisfy
![]()
by matrix multiplication. If we let ![]() , where
, where ![]() is a real number, we have eigenvectors of the form
is a real number, we have eigenvectors of the form ![]() . For
. For ![]() ,
,
![Rendered by QuickLaTeX.com \begin{align*} \lambda I-A&=6\begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}+ (-1)\left[ \begin{array}{@{}*{7}{r}@{}} -2&4\\ 2&5 \\ \end{array} \right]\\ &=\left[ \begin{array}{@{}*{7}{r}@{}} 6&0\\ 0&6 \\ \end{array} \right]+ \left[ \begin{array}{@{}*{7}{r}@{}} 2&-4\\ -2&-5 \\ \end{array} \right]\\ &=\left[ \begin{array}{@{}*{7}{r}@{}} 8&-4\\ -2&1 \\ \end{array} \right] \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-80bf59bfb61404c61182c5cd9459f66d_l3.png)
Using elementary row operations, we get ![]()
The solutions to the equation
![]()
which can be written as
![]()
are ![]() matrices that satisfy
matrices that satisfy
![]()
by matrix multiplication. If we let ![]() , where
, where ![]() is a real number, we have eigenvectors of the form
is a real number, we have eigenvectors of the form ![]() .
.
Therefore, the eigenvalues are
![]()
with corresponding eigenvectors that are nonzero scalar multiples of
![]()
The eigenvalue problem is not the only one that exists in Linear Algebra. There is another one known as the diagonalization problem that we will discuss in the following section.
Diagonalization
The diagonalization problem goes like this: “For a square matrix ![]() , does there exist an invertible matrix
, does there exist an invertible matrix ![]() such that
such that ![]() is diagonal?” [16]. A diagonal matrix is a square matrix where all entries above and below the main diagonal are zeros. So, the only thing differentiating one diagonal matrix from another is what entries are located along the main diagonal. We will see that the diagonalization of a matrix
is diagonal?” [16]. A diagonal matrix is a square matrix where all entries above and below the main diagonal are zeros. So, the only thing differentiating one diagonal matrix from another is what entries are located along the main diagonal. We will see that the diagonalization of a matrix ![]() , if it can be done, will result in a diagonal matrix with the eigenvalues of
, if it can be done, will result in a diagonal matrix with the eigenvalues of ![]() along the main diagonal [16].
along the main diagonal [16].
Let’s look at the formal definition of a diagonalizable matrix as given by Larson and Falvo [16].
An
Once the eigenvalues and corresponding eigenvectors of a matrix ![]() are found, it is not difficult to determine whether
are found, it is not difficult to determine whether ![]() is diagonalizable. It is also not difficult to find the diagonal matrix if
is diagonalizable. It is also not difficult to find the diagonal matrix if ![]() is diagonalizable. We simply have to follow the steps that are given below by Larson and Falvo [16].
is diagonalizable. We simply have to follow the steps that are given below by Larson and Falvo [16].
Let ![]() be an
be an ![]() matrix.
matrix.
- Find
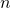 linearly independent eigenvectors
linearly independent eigenvectors 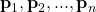 for
for  with corresponding eigenvalues
with corresponding eigenvalues 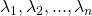 . If
. If 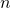 linearly independent eigenvectors do not exist,
linearly independent eigenvectors do not exist,  is not diagonalizable.
is not diagonalizable. - If
 has
has 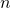 linearly independent eigenvectors, let
linearly independent eigenvectors, let 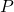 be the
be the 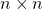 matrix whose columns are these eigenvectors.
matrix whose columns are these eigenvectors. - The diagonal matrix
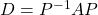 will have the eigenvalues
will have the eigenvalues 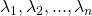 on its main diagonal (and zeros elsewhere). Additionally, the order of the eigenvectors used to form
on its main diagonal (and zeros elsewhere). Additionally, the order of the eigenvectors used to form  will correspond to the order in which the eigenvalues appear on the main diagonal of
will correspond to the order in which the eigenvalues appear on the main diagonal of  .
.
Let’s now work through an example demonstrating these steps. This is a problem I wrote for this paper.
Find a matrix
![]()
and find the matrix ![]()
Solution
By example 67, the eigenvalues of ![]() are -3 and 6 with corresponding eigenvectors
are -3 and 6 with corresponding eigenvectors
![]()
If one of the two eigenvectors could be written as a linear combination of the other, then we would have to find a scalar that could be multiplied by one of the eigenvectors to get the other. It is easy to see that neither can be written as a linear combination of the other. Thus, they are linearly independent, and ![]() is diagonalizable. This concludes the first step.
is diagonalizable. This concludes the first step.
The second step says to let ![]() be the matrix that whose columns are the eigenvectors. So, we have that
be the matrix that whose columns are the eigenvectors. So, we have that
![]()
By step 3, we have that the diagonal matrix ![]() has the eigenvalues along the main diagonal appearing in the same order as their corresponding eigenvectors appear in
has the eigenvalues along the main diagonal appearing in the same order as their corresponding eigenvectors appear in ![]() . So,
. So,
![]()
The solution to the diagonalization problem for ![]() is that there does exist an invertible matrix
is that there does exist an invertible matrix ![]() such that
such that ![]() is diagonal, and
is diagonal, and
![]()
