Newton-Raphson Method

Abigail Huettig

45 Newton-Raphson Method

The Newton-Raphson method allows us to find roots of a nonlinear equation $f(x)$ [9]. That is, this method helps us find $x$ such that $f(x)=0$ .

According to this method,

$x_{r}\approx x_n-\frac{f(x_n)}{f'(x_n)}$

where $x_r$ is a root of $f(x)$ [9]. The reasoning behind this goes back to the Taylor series. According to Hiestand, we start by developing a Taylor series through the first derivative where $f(x)=f(x_r)$ and $f(x_0)=f(x_n)$ [9]. This give us the following equation.

$f(x_r)\approx f(x_n)+f'(x_n)\cdot (x_r-x_n)$

Next, we can suppose that $f(x_r)$ is a root, as long as a root exists [9]. This implies that

$0=f(x_r)\approx f(x_n)+f'(x_n)\cdot (x_r-x_n).$

Finally, we solve for $x_r$ [9].

$\begin{align*} 0&\approx f(x_n)+f'(x_n)\cdot (x_r-x_n)\\ 0&\approx\frac{f(x_n)}{f'(x_n)}+x_r-x_n\\ x_r&\approx x_n-\frac{f(x_n)}{f'(x_n)} \end{align*}$

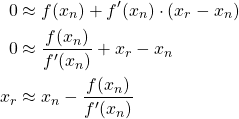
Recall that the closer $x_0$ is to $x$ , the better the approximation of the Taylor series for $f(x)$ is. Knowing this, we want to pick $x_n=x_0$ such that $x_0$ is close to the root, $x_r$ . Then, substituting $x_n=x_0$ into our equation,

$x_r\approx x_0-\frac{f(x_0)}{f'(x_0)}=x_1.$

Because $x_1$ is close to $x_r$ , we can then substitute in $x_1$ to get

$x_r\approx x_1-\frac{f(x_1)}{f'(x_1)}=x_2.$

Because $x_1$ is closer to $x_r$ than $x_0$ is, $x_2$ is a better approximation for $x_r$ than $x_1$ is. We can then get an even closer approximation by substituting $x_2$ into the formula, then $x_3$ , and so on. With each iteration of this process, we are getting closer to $x_r$ .

Well, that’s not entirely true. If $x_0$ is not close enough to the desired root, this process may actually lead us farther away from the root or lead us to another root if more than one exists [9]. Consequently, we need to be careful when choosing $x_0$ .

Let’s now work through an example that demonstrates the Newton-Raphson method. This problem is one I completed for this paper and comes from Hiebert [9].

Example 81
Consider the equation $f(x)=x^3-6x^2+9x-4=0$ . Estimate the smallest root for this equation and use this answer as the starting value to perform three iterations with the Newton-Raphson method.

Solution
If $x$ is negative, $x^3$ , $-6x^2$ , $9x$ , and $-4$ are all negative. Thus, it is impossible for $x$ to be negative and a root. So, every root must be greater than or equal to zero. Thus, the smallest root will be the one closest to zero. So, setting $x_0$ equal to zero seems like a good place to start. We have that

$f'(x)=3x^2-12x+9$

so the iterations are performed as follows.

$\begin{align*} x_1&=0-\frac{0^3-6(0)^2+9(0)-4}{3(0)^2-12(0)+9}\\ &\approx 0.4444 &&\text{First Iteration}\\ x_2&=0.4444-\frac{0.4444^3-6(0.4444)^2+9(0.4444)-4}{3(0.4444)^2-12(0.4444)+9}\\ &\approx 0.7021 &&\text{Second Iteration}\\ x_3&=0.7021-\frac{0.7021^3-6(0.7021)^2+9(0.7021)-4}{3(0.7021)^2-12(0.7021)+9}\\ &\approx 0.8446 &&\text{Third Iteration}\\ \end{align*}$

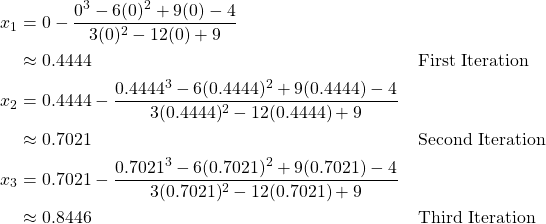
After three iterations, we have

$x_r\approx 0.8446.$

Because

$\begin{align*} f(0.4444)&\approx -1.09758\\ f(0.7021)&\approx -0.29267\\ f(0.8446)&\approx -0.076187,\\ \end{align*}$

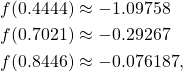
we can see that we are getting closer to a root with each iteration so $x_0=0$ was a good choice.

The Newton-Raphson Method is a great one, but it does have one drawback. We are required to find the derivative. With the example above, it was not difficult to find the first derivative, but not every problem will be that simple. This is the beauty of our next rule, the Secant Rule. It allows us to bypass finding the derivative.

45 Newton-Raphson Method

License

Share This Book