14 Relations
A relation is simply a set of ordered pairs ![]() where
where ![]() and
and ![]() are related in some way [23]. Smith et al. provides us with the following formal definition [23].
are related in some way [23]. Smith et al. provides us with the following formal definition [23].
Let
The definition mentions that ![]() must be a subset of
must be a subset of ![]() if it is a relation from
if it is a relation from ![]() to
to ![]() . The elements of
. The elements of ![]() are of the form
are of the form ![]() , where
, where ![]() is in
is in ![]() and
and ![]() is in
is in ![]() . So, if
. So, if ![]() is a relation from
is a relation from ![]() to
to ![]() , the elements of
, the elements of ![]() will be of the form
will be of the form ![]() . Similarly, if
. Similarly, if ![]() is a relation from
is a relation from ![]() to
to ![]() , the elements of
, the elements of ![]() will be of the form
will be of the form ![]() where
where ![]() and
and ![]() are elements of
are elements of ![]() .
.
Domain and range are terms that we will be using many times in the coming sections so it is important to understand what these terms are referring to. The following definition comes from Smith et al.[23].
The domain of the relation
![]()
The range of the relation ![]() is the set
is the set
![]()
In other words, for a relation from ![]() to
to ![]() , the domain of the relation is the set of all
, the domain of the relation is the set of all ![]() in
in ![]() that are related to at least one
that are related to at least one ![]() in
in ![]() . Similarly, the range of the relation is the set of all
. Similarly, the range of the relation is the set of all ![]() in
in ![]() that are related to at least one
that are related to at least one ![]() in
in ![]() .
.
There are many different properties that can be used to describe a relation, and we can categorize relations based on the properties they possess. These categories include equivalence relations and ordering relations.
Equivalence Relations
An equivalence relation is a special type of relation that is reflexive, symmetric, and transitive [23]. Smith et al. provides the following definition [23].
Let
-
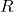 is reflexive on
is reflexive on  if for all
if for all 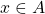 ,
, 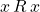 .
. -
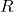 is symmetric if for all
is symmetric if for all 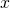 and
and 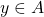 , if
, if 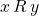 ,
, 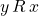 .
. -
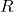 is transitive if for all
is transitive if for all 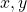 , and
, and 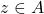 , if
, if 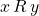 and
and 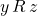 , then
, then 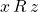 .
.
The reflexive property simply means that every ![]() in
in ![]() must be related to itself. The symmetric property says that for each
must be related to itself. The symmetric property says that for each ![]() and
and ![]() in
in ![]() ,
, ![]() must be related to
must be related to ![]() if
if ![]() is related to
is related to ![]() . Transitive simply means that for each
. Transitive simply means that for each ![]() , and
, and ![]() in
in ![]() , if
, if ![]() is related to
is related to ![]() and
and ![]() is related to
is related to ![]() , then
, then ![]() must be related to
must be related to ![]() . Let’s look at an example to see what these properties look like for a specific relation. The following exercise is a homework problem from Smith et al. that I completed for this paper [23].
. Let’s look at an example to see what these properties look like for a specific relation. The following exercise is a homework problem from Smith et al. that I completed for this paper [23].
Determine whether the relation
Solution
- For all
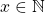 ,
, 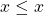 . Thus,
. Thus, 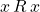 , and
, and 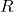 is reflexive.
is reflexive. - For all
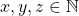 , if
, if 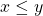 and
and 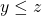 , then
, then 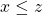 . So, if
. So, if 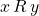 and
and 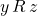 , then
, then 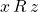 . Thus,
. Thus,  is transitive.
is transitive. - However, there exists
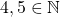 such that if
such that if  , then
, then 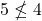 . Thus,
. Thus,  is not symmetric.
is not symmetric.
Therefore, the relation ![]() is not an equivalence relation.
is not an equivalence relation.
Ordering Relations
We will start this section by defining three more properties of relations. The following definition comes from Smith et al. [23].
Let
-
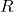 is antisymmetric if for all
is antisymmetric if for all 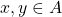 , if
, if 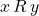 and
and 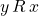 , then
, then 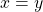 .
. -
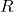 is irreflexive on
is irreflexive on  if
if 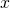 is not related to
is not related to 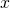 for all
for all 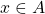 .
. -
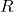 has the comparability property if for all
has the comparability property if for all 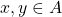 , either
, either 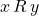 or
or 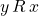 .
.
Antisymmetric means that for each ![]() and
and ![]() in
in ![]() where
where ![]() , the symmetric property cannot hold. Similarly, the irreflexive property means that for each
, the symmetric property cannot hold. Similarly, the irreflexive property means that for each ![]() in
in ![]() the reflexive property cannot hold. That is,
the reflexive property cannot hold. That is, ![]() is not related to itself. Finally, the comparability property says that for each
is not related to itself. Finally, the comparability property says that for each ![]() and
and ![]() in
in ![]() , it must be true that either
, it must be true that either ![]() is related to
is related to ![]() or
or ![]() is related to
is related to ![]() .
.
Using these additional properties, we have more categories that we can organize relations into. These categories are given by Smith et al. A relation is a partial order or partial ordering if it is reflexive, antisymmetric, and transitive. A relation is a strict partial order or strict partial ordering if it is irreflexive, antisymmetric, and transitive. A partial ordering is called a linear order or total order if the comparability property holds for all ![]() and
and ![]() in
in ![]() where
where ![]() [23]. We will now look at a homework problem from Smith et al. that I completed for this paper [23].
[23]. We will now look at a homework problem from Smith et al. that I completed for this paper [23].
Determine what kind of relation
Solution
- For all
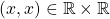 ,
, 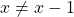 . Thus,
. Thus, 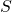 is irreflexive.
is irreflexive. - For all
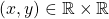 ,
,
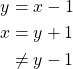
Thus,
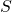 is antisymmetric.
is antisymmetric. - There exists
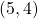 and
and 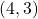 in
in 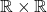 such that
such that 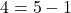 and
and 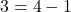 but
but 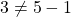 . Thus,
. Thus, 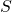 is not transitive.
is not transitive. - There exists
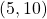 in
in 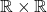 such that
such that 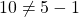 and
and 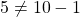 . Thus, the comparability property does not hold for
. Thus, the comparability property does not hold for 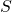 .
.
Therefore, ![]() is not an equivalence relation because it is not reflexive, symmetric, or transitive. It is not a partial ordering because it is not reflexive or transitive. It is also not a strict partial ordering since it is not transitive, and it is not a linear order since it is not a partial ordering and the comparability property does not hold for all
is not an equivalence relation because it is not reflexive, symmetric, or transitive. It is not a partial ordering because it is not reflexive or transitive. It is also not a strict partial ordering since it is not transitive, and it is not a linear order since it is not a partial ordering and the comparability property does not hold for all ![]() and
and ![]() , where
, where ![]() .
.
Up to this point, we have discussed types of relations from ![]() to
to ![]() , where
, where ![]() is a set. In our next section, we will discuss another type of relation, known as a function, which may be a relation from
is a set. In our next section, we will discuss another type of relation, known as a function, which may be a relation from ![]() to
to ![]() or from
or from ![]() to
to ![]() , where
, where ![]() and
and ![]() are distinct sets.
are distinct sets.
