26 Rings of Polynomials
A ring of polynomials ![]() is a ring consisting of all polynomials with coefficients in the ring
is a ring consisting of all polynomials with coefficients in the ring ![]() [7]. Similarly, the set of polynomials over a field
[7]. Similarly, the set of polynomials over a field ![]() , denoted
, denoted ![]() , consists of all polynomials with coefficients in the field
, consists of all polynomials with coefficients in the field ![]() [17].
[17].
One idea we are often interested in is whether a particular polynomial can be factored over a given field. Consider the following definition by Macauley [17].
A polynomial
We are already familiar with this idea. Whenever we factored a polynomial in a high-school math class, that polynomial was reducible over the field ![]() because every coefficient was a real number. Now, we are generalizing this same process to apply to any field.
because every coefficient was a real number. Now, we are generalizing this same process to apply to any field.
Let’s look at an example to demonstrate this. This is a problem I completed for this paper that comes from Fraleigh and Katz [7].
The polynomial
Solution
Since we are in ![]() , addition is defined as
, addition is defined as ![]() mod(5) and multiplication as
mod(5) and multiplication as ![]() mod(5). So, we have
mod(5). So, we have
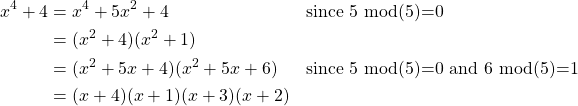
Therefore, ![]() in
in ![]() .
.
In the example above, we see that each factor is of a degree less than 4 and has coefficients that are elements of ![]() , which is consistent with definition V.14.
, which is consistent with definition V.14.
As was also seen in high-school math classes, not every polynomial can be factored. Such polynomials are said to be irreducible.
Irreducibility
Sometimes, a polynomial ![]() is not reducible over a field
is not reducible over a field ![]() . In this case, we say that
. In this case, we say that ![]() is irreducible over
is irreducible over ![]() [17].
[17].
One theorem, along with its corollary, is very helpful in determining if a polynomial is irreducible. Both the theorem and corollary are given by Fraleigh and Katz as follows [7].
Theorem V.15
Corollary V.15.1
These will make more sense after looking at an example that utilizes them. The following problem is one I completed for this paper and comes from Fraleigh and Katz [7].
Show that
Proof.
If we could reduce ![]() over
over ![]() , then
, then ![]() would either have a cubic factor and a linear factor or two quadratic factors. This is because
would either have a cubic factor and a linear factor or two quadratic factors. This is because ![]() and
and ![]() . So, to multiply two factors together to get
. So, to multiply two factors together to get ![]() , we need either
, we need either
![]()
or
![]()
We will now show why neither of these options is possible.
Suppose ![]() has a linear factor in
has a linear factor in ![]() . That is,
. That is,
![]()
where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are rationals. If
are rationals. If ![]() , we have
, we have
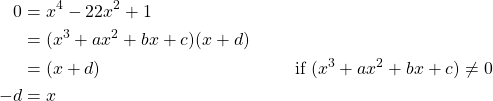
So, ![]() is a zero, and
is a zero, and ![]() is rational because
is rational because ![]() and
and ![]() are rational and
are rational and ![]() is closed under multiplication. This means
is closed under multiplication. This means ![]() has a zero in
has a zero in ![]() and thus, a zero in
and thus, a zero in ![]() that must divide 1 by corollary V.15.1. So,
that must divide 1 by corollary V.15.1. So, ![]() or
or ![]() must be a zero. But,
must be a zero. But,
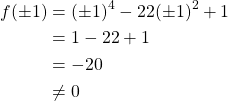
Because ![]() does not have a zero that divides 1, we have a contradiction of corollary V.15.1, and this factorization is impossible.
does not have a zero that divides 1, we have a contradiction of corollary V.15.1, and this factorization is impossible.
Now suppose that ![]() has two quadratic factors in
has two quadratic factors in ![]() . By Theorem V.15,
. By Theorem V.15, ![]() has a factorization of the form
has a factorization of the form ![]() in
in ![]() . Expanding this, we have
. Expanding this, we have
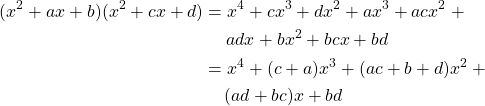
Because our original polynomial is ![]() , we have
, we have
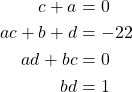
Because ![]() and
and ![]() and
and ![]() are integers, it follows that
are integers, it follows that ![]() . So, we have
. So, we have
![]()
If ![]() ,
, ![]() If
If ![]() ,
, ![]() This implies
This implies ![]() is negative and
is negative and ![]() is positive or vice versa. Because
is positive or vice versa. Because ![]() ,
,
![]()
However, there do not exist ![]() such that
such that ![]() and
and ![]() or
or ![]() . Thus, this factorization is impossible as well. Therefore,
. Thus, this factorization is impossible as well. Therefore, ![]() is irreducible over
is irreducible over ![]() .
.
The process we used in this example cannot always be used, and even if it could, it is a long, inefficient method. There has got to be a better way, and in fact, there is, known as the Eisenstein Criterion.
Eisenstein Criterion
The Eisenstein Criterion is given by Macauley as follows [17].
Theorem V.16 (Eisenstein Criterion)
-
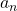 is not divisible by
is not divisible by 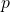 .
. -
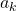 , for
, for  , is divisible by
, is divisible by 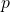 .
. -
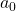 is not divisible by
is not divisible by 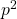 .
.
Keep in mind that the Eisenstein Criterion only applies to polynomials with integer coefficients. If we can find a prime number ![]() that divides every coefficient except the first one that, when squared, does not divide the last one, then the polynomial is irreducible. Let’s look at the following problem that I completed for this paper and comes from Fraleigh and Katz [7].
that divides every coefficient except the first one that, when squared, does not divide the last one, then the polynomial is irreducible. Let’s look at the following problem that I completed for this paper and comes from Fraleigh and Katz [7].
Determine whether the polynomial
Solution
We have that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() be the prime number 5. Because
be the prime number 5. Because
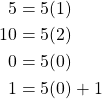
we have that ![]() ,
, ![]() , and
, and ![]() are divisible by 5, but
are divisible by 5, but ![]() is not divisible by 5. Thus, the first and second conditions of the criterion are satisfied. Furthermore,
is not divisible by 5. Thus, the first and second conditions of the criterion are satisfied. Furthermore,
![]()
so ![]() is not divisible by
is not divisible by ![]() . Therefore,
. Therefore, ![]() in
in ![]() satisfies an Eisenstein criterion for irreducibility over
satisfies an Eisenstein criterion for irreducibility over ![]() .
.
