Secant Rule

Abigail Huettig

44 Secant Rule

The Secant Rule is an alternative to the Newton-Raphson method that does not require that we find the first derivative [9]. The benefit of the Secant Rule is that we can use it when the derivative would be difficult to find. However, the drawback is that this rule may take a few more iterations than the Newton-Raphson method to get to the same answer [9]. The Secant Rule formula is given by Hiestand as follows [9]:

$x_{n+1}=x_n-\frac{f(x_n)\cdot (x_n-x_{n-1})}{f(x_n)-f(x_{n-1})}.$

The reasoning behind the Secant Rule is that we approximate the derivative rather than find the exact derivative function. Recall from Part I: Chapter 2 that the definition of the derivative of a function $f(x)$ is

$f'(x)=\lim_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}.$

First, we let $x=x_{n-1}$ and $x+\Delta x=x_n$ [9]. Then we have

$f'(x)=\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}.$

Finally, we substitute $f'(x)$ into the Newton-Raphson equation [9].

$\begin{align*} x_{n+1}&=x_n-\frac{f(x_n)}{\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}}\\ &=x_n-\frac{f(x_n)\cdot (x_n-x_{n-1})}{f(x_n)-f(x_{n-1})} \end{align*}$

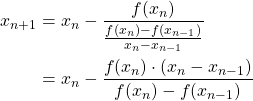
Now we have our formula for the Secant Rule. Notice that with this formula we need two starting values as opposed to just one. A good way to find these values is to find the starting value that we would use for the Newton-Raphson method. Then pick another number that is very close to that starting value.

Let’s now work through an example demonstrating this rule. This problem is one I completed for this paper and comes from Hiestand [9].

Example 82
Consider the equation $f(x)=x^3-6x^2+9x-4=0$ . Estimate the largest root of this equation and use this answer to perform three iterations with the secant rule.

Solution
For $x\geq 6$ , $x^3-6x^2\geq 0$ and $9x-4>0.$ It follows that $f(x)>0$ for $x\geq 6$ . This means that any root would have to be less than six. So, we will let $x_0=6$ and $x_1=5.99.$ Our first three iterations are then

$\begin{align*} x_2&=5.99-\frac{f(5.99)\cdot (5.99-6)}{f(5.99)-f(6)}\\ &\approx 5.99-\frac{49.5512\cdot (-0.01)}{49.5512-50}\\ &\approx 4.88592 \end{align*}$

$\begin{align*} x_3&=4.88592-\frac{f(4.88592)\cdot (4.88592-5.99)}{f(4.88592)-f(5.99)}\\ &\approx 4.88592-\frac{13.3777\cdot (-1.10408)}{13.3777-49.5512}\\ &\approx 4.47761 \end{align*}$

$\begin{align*} x_4&=4.47761-\frac{f(4.47761)\cdot (4.47761-4.88592)}{f(4.47761)-f(4.88592)}\\ &\approx 4.47761-\frac{5.77611\cdot (-0.40831)}{5.77611-13.3777}\\ &\approx 4.16735 \end{align*}$

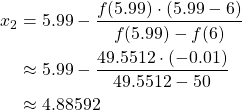
After three iterations,

$x_r\approx 4.16735.$

Because

$\begin{align*} f(4.88592)&\approx 13.3777\\ f(4.47761)&\approx 5.77611\\ f(4.16735)&\approx 1.67887,\\ \end{align*}$

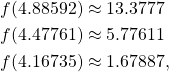
we are getting closer to a root with each iteration so $x_0=6$ and $x_1=5.99$ were good choices.

If we continued on, we would eventually reach our root. But since we understand how the Secant Rule works, let’s move on to our last topic, Gaussian-Seidel Iteration.

44 Secant Rule

License

Share This Book