6 Sequences
Abbott provides us with the following definition for a sequence [1].
A sequence is a function whose domain is
So, a sequence ![]() defined by a function
defined by a function ![]() is really just a number pattern where
is really just a number pattern where ![]() is the
is the ![]() th term
th term ![]() in the pattern. In calculus, we are interested in whether the sequence converges or diverges (does not converge).
in the pattern. In calculus, we are interested in whether the sequence converges or diverges (does not converge).
One way to find whether a sequence ![]() defined by
defined by ![]() converges is to find
converges is to find
![]()
If this limit exists, then the sequence not only converges but converges to that limit [15].
We also have a theorem that can be used to determine if a sequence converges when it is hard to find the limit or to know if it even exists. The theorem is stated by Larson and Edwards as follows [15].
Theorem I.13
This theorem raises an important question. What do bounded and monotonic mean?
A sequence is bounded above when ![]() is less than or equal to a real number
is less than or equal to a real number ![]() for all
for all ![]() and bounded below when
and bounded below when ![]() is greater than or equal to
is greater than or equal to ![]() for all
for all ![]() . A sequence is bounded when it is bounded above and below [15].
. A sequence is bounded when it is bounded above and below [15].
Monotonic means that either
![]()
for all ![]() [15]. That is, the sequence is either nondecreasing or nonincreasing.
[15]. That is, the sequence is either nondecreasing or nonincreasing.
We will not go through a formal proof here, but we will discuss why this theorem makes sense. Consider a nondecreasing, bounded sequence ![]() . That is,
. That is,
![]()
where ![]() is a real number. Every sequence must either converge or diverge, and a nondecreasing sequence diverges if and only if for every real number
is a real number. Every sequence must either converge or diverge, and a nondecreasing sequence diverges if and only if for every real number ![]() we can find
we can find ![]() such that
such that ![]() . Because there exists a real number
. Because there exists a real number ![]() such that
such that ![]() for all
for all ![]() ,
, ![]() does not diverge and must converge. Thus, if a sequence is nondecreasing and bounded, it must converge. Similar reasoning can be used for a nonincreasing, bounded sequence.
does not diverge and must converge. Thus, if a sequence is nondecreasing and bounded, it must converge. Similar reasoning can be used for a nonincreasing, bounded sequence.
Let’s now look at a problem that demonstrates how to prove a sequence is monotone and bounded so that the theorem can be applied. This is a problem I completed for Calculus II and comes from Larson and Edwards [15].
Does
Solution
The terms of ![]() are
are
![]()
The terms appear to be decreasing but will the sequence continue this way? Because ![]() is positive, we have that for all
is positive, we have that for all ![]()

Thus, ![]() is decreasing and consequently monotonic. Moreover,
is decreasing and consequently monotonic. Moreover, ![]() is bounded above by 13.
is bounded above by 13.
Now, we need to determine if ![]() is bounded below. Because
is bounded below. Because ![]() is a natural number, we have
is a natural number, we have
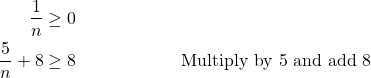
Thus, ![]() is bounded below by 8. By Theorem I.13,
is bounded below by 8. By Theorem I.13, ![]() converges.
converges.
We are now going to begin our discussion of series, which builds upon the ideas of sequences.
