7 Series
A series is written as
![]()
and the definitions of convergent and divergent series are stated by Larson and Edwards as follows [15].
For the infinite series
![]()
If the sequence of partial sums ![]() converges to
converges to ![]() , then the series
, then the series ![]() converges. The limit
converges. The limit ![]() is called the sum of the series.
is called the sum of the series.
![]()
If ![]() diverges, then the series diverges.
diverges, then the series diverges.
As with sequences, we are concerned with whether a series converges or diverges. There are some types of series that have their own set of rules for whether they converge or not, such as geometric series and p-series. If a series is not one of these special types, then we have tests that can be used to determine convergence, such as the Direct Comparison and Alternating Series tests.
Geometric Series
A geometric series is a special type of series. Not only is it easy to tell whether such a series converges or diverges, but it is also easy to find the sum that the series converges to. Let’s look at the following theorem and proof from Larson and Edwards [15].
Theorem I.15 (Convergence of a Geometric Series)
![]()
Proof.
It is easy to see that the series diverges when ![]() If
If ![]() , then we have the partial sum
, then we have the partial sum
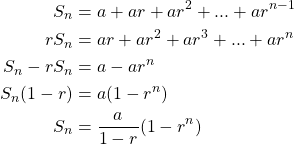
When ![]() , it follows that
, it follows that ![]() . So,
. So,
![]()
Thus, the series converges, and its sum is ![]() .
.
When ![]() , it follows that
, it follows that ![]() alternates between
alternates between ![]() and
and ![]() , and when
, and when ![]() , it follows that
, it follows that ![]() . So if
. So if ![]()
![]()
Thus, the limit does not exist, and the series diverges.
Let’s now do an example I completed for Calculus II that comes from Larson and Edwards [15].
Does the series
We have that
![]()
by Theorem I.15.
Another special type of series for which it is easy to determine convergence and divergence is the ![]() -series.
-series.
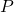 -series
-series
Consider the following theorem provided by Larson and Edwards [15].
Theorem I.16
![]()
converges for ![]() and diverges for
and diverges for ![]() .
.
Let’s now look at how to use this theorem. This problem is one I completed for Calculus II and comes from Larson and Edwards [15].
Example 16
Does ![]() converge or diverge?
converge or diverge?
Solution
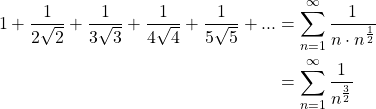
Since ![]() and
and ![]() , this series converges by Theorem I.16.
, this series converges by Theorem I.16.
Because many series do not fall into nice categories such as geometric series and ![]() -series, we need tests that we can use to help us determine convergence and divergence.
-series, we need tests that we can use to help us determine convergence and divergence.
Direct Comparison Test
The first test for convergence and divergence that we are going to discuss is the direct comparison test. This test is stated as a theorem by Larson and Edwards as follows [15].
Theorem I.17
Let ![]() for all
for all ![]() .
.
- If
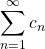 converges, then
converges, then 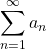 converges.
converges. - If
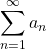 diverges, then
diverges, then 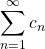 diverges.
diverges.
Proof.
To prove the first part, let ![]() and let
and let
![]()
and
![]()
Since ![]() ,
, ![]() converges to
converges to ![]() by Definition I.14. Additionally, because
by Definition I.14. Additionally, because ![]() for all
for all ![]() , we have
, we have
![]()
and
![]()
So, the sequence ![]() is bounded above. Because
is bounded above. Because ![]() ,
, ![]() is also increasing and thus bounded below by
is also increasing and thus bounded below by ![]() . By Theorem I.13,
. By Theorem I.13, ![]() converges, and
converges, and ![]() converges by Definition I.14.
converges by Definition I.14.
Therefore, if ![]() for all
for all ![]() and
and ![]() converges,
converges, ![]() converges as well. Because part 2 is the contrapositive statement of part 1, part 2 is also true. (See Part II: Chapter 11.)
converges as well. Because part 2 is the contrapositive statement of part 1, part 2 is also true. (See Part II: Chapter 11.)
This proof is one I completed as a challenge for myself with some help from the proof given for this test in Larson and Edwards [15]. Let’s now work through an example I completed for Calculus II that comes from Larson and Edwards [15].
Example 17
Using the Direct Comparison Test, does ![]() converge or diverge?
converge or diverge?
Solution
The series
![]()
looks very similar to the geometric series
![]()
We know that this geometric series converges by Theorem I.15 so the Direct Comparison test will help us only if for all ![]() ,
,
![]()
We can show this is true the following way.
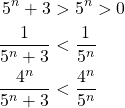
Because ![]() for all
for all ![]() and
and ![]() converges,
converges, ![]() converges by the Direct Comparison Test.
converges by the Direct Comparison Test.
We are now going to discuss one other test, the alternating series test, before concluding our discussion of series.
Alternating Series Test
The alternating series test helps us determine if a series is converging. Larson and Edwards state the test as follows [15].
Theorem I.18 (Alternating Series Test)
Let ![]() . The alternating series
. The alternating series
![]()
converge when the two conditions listed below are met.
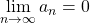
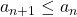 , for all
, for all 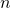
Proof.
Consider the alternating series ![]() . For this series, the partial sum (where
. For this series, the partial sum (where ![]() is even)
is even)
![]()
has all nonpositive terms because ![]() , and therefore
, and therefore ![]() is a nonincreasing sequence. But the partial sum can be rewritten as
is a nonincreasing sequence. But the partial sum can be rewritten as
![]()
which implies that ![]() for every integer
for every integer ![]() (because
(because ![]() ). So,
). So, ![]() is a bounded, nonincreasing sequence that converges to some value
is a bounded, nonincreasing sequence that converges to some value ![]() by Theorem I.13. Notice that
by Theorem I.13. Notice that ![]() . Because
. Because ![]() ,
, ![]() So we have,
So we have,
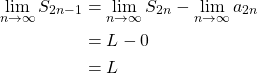
Because both ![]() and
and ![]() converge to the same limit
converge to the same limit ![]() , it follows that
, it follows that ![]() also converges to
also converges to ![]() . Consequently, the given alternating series converges by Definition I.14.
. Consequently, the given alternating series converges by Definition I.14.
This proof is one I completed for Calculus II. The proof for when the series is
![]()
can be done in a similar manner and is found in Larson and Edwards [15]. Let’s now work through an example I completed for Calculus II that comes from Larson and Edwards [15].
Example 18
Does ![]() converge or diverge?
converge or diverge?
Solution
Because
![]()
and ![]() , we need to check the two conditions of the Alternating Series test to see if this test applies. Because
, we need to check the two conditions of the Alternating Series test to see if this test applies. Because
![]()
the first condition holds. Additionally, because
![]()
for all ![]() , the second condition holds. Therefore,
, the second condition holds. Therefore, ![]() converges by the Alternating Series Test.
converges by the Alternating Series Test.
Our final calculus topic we will discuss is differential equations. Differential equations contain derivatives within them, and in order to solve them, we must use integration. There is so much we could discuss, but we are going to settle with one specific type, the separable differential equation.
