46 Simpson’s Rules
Similar to the rectangle method, the trapezoid rule becomes more accurate if we partition the interval ![]() into smaller intervals, resulting in more trapezoids. However, this can become complicated when we have a large number of trapezoids. Thankfully, Simpson’s rules provide us with a better method for finding a more accurate approximation of the area than the trapezoid rule can provide [9].
into smaller intervals, resulting in more trapezoids. However, this can become complicated when we have a large number of trapezoids. Thankfully, Simpson’s rules provide us with a better method for finding a more accurate approximation of the area than the trapezoid rule can provide [9].
Consider the following diagram.
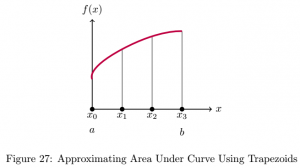
Simpson’s rules connect ![]() to
to ![]() with a parabola rather than a straight line [9]. This gives a better approximation than the trapezoid rule because there is even less space between the parabolas and the curve than there was between the trapezoids and the curve.
with a parabola rather than a straight line [9]. This gives a better approximation than the trapezoid rule because there is even less space between the parabolas and the curve than there was between the trapezoids and the curve.
Simpson’s 1/3 Rule
This rule can be used only when we have partitioned ![]() into an even number of intervals [9]. The formula is given by Hiestand as follows [9]:
into an even number of intervals [9]. The formula is given by Hiestand as follows [9]:
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \int_a^b f(x)\, dx&=\frac{\Delta x}{3}\cdot [f(a)+4\cdot f(a+\Delta x)+2\cdot f(a+2\Delta x)\\ &+4\cdot f(a+3\Delta x)+2\cdot f(a+4\Delta x)+...\\ &+2\cdot f(b-2\Delta x)+4\cdot f(b-\Delta x)+f(b)] \end{split} \end{equation*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b375ea6ab617d1b4147649f7c7c2b2a3_l3.png)
Before working through an example, we will briefly discuss the second of Simpson’s rules.
Simpson’s 3/8 Rule
This rule can be used only when we have partitioned ![]() into three intervals [9]. The formula is given by Hiestand as follows [9]:
into three intervals [9]. The formula is given by Hiestand as follows [9]:
(2) ![]()
Because this formula works only for three intervals, we will need to use both the ![]() rule and
rule and ![]() rule when we have
rule when we have ![]() intervals where
intervals where ![]() is odd and greater than three. This can be done by breaking the integral into two integrals using the following equation:
is odd and greater than three. This can be done by breaking the integral into two integrals using the following equation:
![]()
Either ![]() or
or ![]() is partitioned into three intervals while the other is partitioned into
is partitioned into three intervals while the other is partitioned into ![]() intervals [9].
intervals [9].
Let’s look at an example to better understand how this works. The following problem is one I completed for this paper and comes from Hiestand [9].
Consider the integral
![]()
Evaluate the integral using Simpson’s rules with ![]() throughout.
throughout.
Solution
Using ![]() , the intervals that we partition
, the intervals that we partition ![]() into are
into are
![]()
and
![]()
Because we have seven intervals, we will need to use both the ![]() rule and the
rule and the ![]() rule. First, we need to split our integral into two integrals. One way to do this is
rule. First, we need to split our integral into two integrals. One way to do this is
![]()
Substituting into equation 1 above, we have
![Rendered by QuickLaTeX.com \begin{align*} \int_0^{0.5} \sqrt{1-x^2}\, dx&=\frac{0.125}{3}\cdot [f(0)+4\cdot f(0.125)+2\cdot f(0.25)\\ &+4\cdot f(0.375)+ f(0.5)]\\ &\approx 0.041667\cdot [1+4(0.992157)+2(0.968246)+4(0.927025)+0.866025]\\ &\approx 0.478306 \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4f57c074a98f9887795a47bc23d82fce_l3.png)
Substituting into equation 2 above, we have
![Rendered by QuickLaTeX.com \begin{align*} \int_{0.5}^{0.875} \sqrt{1-x^2}\, dx&=\frac{(0.875-0.5)\cdot[f(0.5)+3\cdot f(0.625)+3\cdot f(0.75)+f(0.875)]}{8}\\ &\approx \frac{0.375\cdot [0.866025+3(0.780625)+3(0.661438)+0.484123]}{8}\\ &\approx 0.266078\\ \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ed768260e5316fbca30aa6669e0b454f_l3.png)
Therefore,
![]()
Similar to the Trapezoid Rule, we can calculate the maximum and average errors of Simpson’s Rules.
Simpson’s Rules Errors
Calculating the maximum and average errors for Simpson’s rules is very similar to calculating these errors for the trapezoid rule.
The formula for the truncation error for the ![]() rule is given by Hiestand as follows [9].
rule is given by Hiestand as follows [9].
(3) ![]()
To find the maximum error, we choose ![]() in the interval
in the interval ![]() such that the absolute value of
such that the absolute value of ![]() is greater than or equal to the absolute value of
is greater than or equal to the absolute value of ![]() for all
for all ![]() in
in ![]() [9]. Then, we substitute
[9]. Then, we substitute ![]() for
for ![]() in equation 3 above giving us
in equation 3 above giving us
(4) ![]()
To find the average error, we substitute
![]()
for ![]() in equation 3 because
in equation 3 because
![]()
gives us the average of the ![]() th derivative of a function over the interval
th derivative of a function over the interval ![]() [9]. So, we have the following equation:
[9]. So, we have the following equation:
(5) 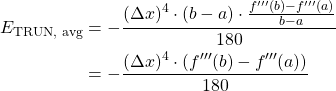
For the ![]() rule, we find the maximum and the average errors the exact same way, only with a different truncation error formula. This formula is given by Hiestand as follows [9]:
rule, we find the maximum and the average errors the exact same way, only with a different truncation error formula. This formula is given by Hiestand as follows [9]:
(6) ![]()
Using this equation, we have the following equation for the maximum error
(7) ![]()
and this equation for the average error
(8) 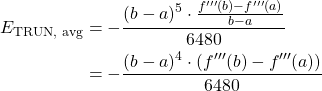
Because the method of finding the maximum and average errors of these rules is similar to finding the maximum and average errors for the Trapezoid Rule, we will not go through another example here. Instead, we are going to move on to the Newton-Raphson method.
