Taylor Series

Abigail Huettig

42 Taylor Series

A Taylor Series is a series (see Part I: Chapter 7) that allows us to approximate the value of a function $f(x)$ at a specific $x$ using the derivatives (see Part I: Chapter 2) of $f$ and one other $x$ value [9]. The general form is given by Hiestand as follows [9].

$f(x)=f(x_0)+f'(x_0)\cdot (x-x_0)+\frac{1}{2!}\cdot f''(x_0)\cdot (x-x_0)^2+...+\frac{1}{n!}\cdot f^n(x_0)\cdot (x-x_0)^n+R_n$

We have some freedom with this method in that we get to choose $x_0$ and $n$ . However, our decisions for these values will affect the accuracy of the final approximation. First, $x_0$ should be chosen so that it is not far from $x$ . The farther $x_0$ is from $x$ , the less accurate the approximation will be [9]. Second, the larger $n$ is, the more accurate the approximation will be [9]. However, the larger $n$ is, the more complicated and time-consuming the computation, especially when doing it by hand. So, we want to choose $n$ small enough that the problem is not too long and complicated but large enough that the approximation is fairly accurate.

$R_n$ is known as the remainder term and is essentially the error between the exact value and approximated value of $f(x)$ . If the exact value is known, $R_n$ can easily be calculated by subtracting the approximate value from the exact value. But usually, the exact value is not known. (If we know the exact value, there is not much of a point in using the Taylor series in the first place.) So, there is a formula for calculating $R_n$ which is given by Hiestand as follows [9].

(1) $\begin{align*} R_n=\frac{1}{(n+1)!}\cdot f^{n+1}(z)\cdot (x-x_0)^{n+1} \end{align*}$

$R_n$ looks just like the next term in the series if we were to go past $n$ with one key difference, the $n$ th+1 derivative is evaluated at $z$ rather than $x_0$ . We want to choose $z$ such that $x_0\leq z\leq x$ and the absolute value of $f^{n+1}(z)$ is as large as possible. This is known as bounding the error [9]. If we choose $z$ in this way, we will have $R_n$ equal to the largest possible error. In other words, we have found the worst case scenario.

We are now going to go through an example I completed for this paper that comes from Hiestand [9].

Example 76
Let $f(x)=x^{\frac{1}{3}}$ .

Develop a Taylor series through the third derivative term for this function.
Use your series to estimate the cube root of 300 by expanding about $x_0=343$ .
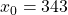Bound the error of your estimate and compare it to the true error.

Solution
We have that

$\begin{align*} f'(x)&=\frac{1}{3}x^{-\frac{2}{3}}\\ f''(x)&=-\frac{2}{9}x^{-\frac{5}{3}}\\ f'''(x)&=\frac{10}{27}x^{-\frac{8}{3}} \end{align*}$

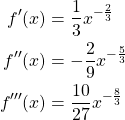
Substituting our derivatives into the Taylor Series equation above, we have the following:

$f(x)\approx f(x_0)+\frac{1}{3}x_0^{-\frac{2}{3}}\cdot (x-x_0)+\frac{1}{2!}\cdot -\frac{2}{9}x_0^{-\frac{5}{3}}\cdot (x-x_0)^2+\frac{1}{3!}\cdot\frac{10}{27}x_0^{-\frac{8}{3}}\cdot (x-x_0)^3.$

Next, we estimate the cube root of $x=300$ by expanding about $x_0=343$ by substituting these values into $f(x)$ .

$\begin{align*} f(300)&\approx f(343)+\frac{1}{3}343^{-\frac{2}{3}}\cdot (300-343)+\frac{1}{2!}\cdot -\frac{2}{9}343^{-\frac{5}{3}}\cdot (300-343)^2\;+\\ &\,\quad \frac{1}{3!}\cdot\frac{10}{27}343^{-\frac{8}{3}}\cdot (300-343)^3\\ &= 7+\frac{1}{147}\cdot (-43)+\frac{1}{2}\cdot \frac{-2}{151,263}\cdot (-43)^2+\frac{1}{6}\cdot \frac{10}{155,649,627}\cdot (-43)^3\\ &\approx 7-0.292517-0.012224-0.000851\\ &=6.69441 \end{align*}$

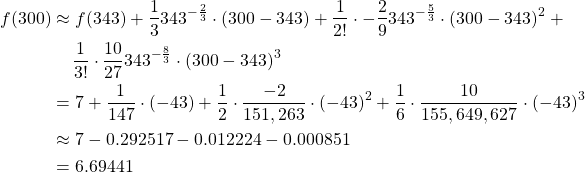
Finally, we need to bound the error of our estimate and compare it to the true error. The fourth derivative of our function evaluated at $z$ is

$f^{(4)}(z)=-\frac{80}{81}z^{-\frac{11}{3}}.$

The value for $z$ between 300 and 343 that gives us the largest absolute value of $f^{(4)}(z)$ is $z=300$ . Substituting into equation 1 above, we have

$\begin{align*} R_3&=\frac{1}{4!}\cdot f^{(4)}(300)\cdot (-43)^{4}\\ &=\frac{1}{24}\cdot -\frac{80}{81}\cdot 300^{-\frac{11}{3}}\cdot (-43)^{4}\\ &\approx -0.000116 \end{align*}$

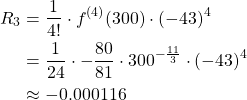
The exact error is

$\begin{align*} |f(300)-6.69441|&=|6.69433-6.69441|\\ &=0.000078 \end{align*}$

Therefore, we have that

$|R_3|\approx 0.000116>0.000078$

It makes sense that the actual error is less than $R_3$ since we chose $z$ such that $|R_3|$ would be the biggest possible error.

This is the process of approximating the output of a function along with the error using a Taylor series. In our next section, we will approximate an integral using the Trapezoid Rule.

42 Taylor Series

License

Share This Book